Zachování vašeho soukromí je pro nás důležité. Z tohoto důvodu jsme vyvinuli Zásady ochrany osobních údajů, které popisují, jak používáme a uchováváme vaše informace. Přečtěte si prosím naše zásady ochrany osobních údajů a dejte nám vědět, pokud máte nějaké dotazy.

Shromažďování a používání osobních údajů

Osobní údaje jsou údaje, které lze použít k identifikaci nebo kontaktování konkrétní osoby.

Kdykoli nás budete kontaktovat, můžete být požádáni o poskytnutí svých osobních údajů.

Níže jsou uvedeny některé příklady typů osobních údajů, které můžeme shromažďovat, a jak takové informace můžeme používat.

Jaké osobní údaje shromažďujeme:

• Když odešlete žádost na stránce, můžeme shromažďovat různé informace, včetně vašeho jména, telefonního čísla, adresy E-mailem atd.

Jak používáme vaše osobní údaje:

• Shromážděno námi osobní informace nám umožňuje kontaktovat vás a informovat vás o jedinečných nabídkách, akcích a dalších akcích a připravovaných akcích.
• Čas od času můžeme použít vaše osobní údaje k zasílání důležitých oznámení a sdělení.
• Osobní údaje můžeme také používat pro interní účely, jako je provádění auditů, analýzy dat a různé výzkumy, abychom zlepšili služby, které poskytujeme, a abychom vám poskytli doporučení týkající se našich služeb.
• Pokud se účastníte slosování o ceny, soutěže nebo podobné propagační akce, můžeme vámi poskytnuté informace použít ke správě takových programů.

Zpřístupnění informací třetím stranám

Informace, které od vás obdržíme, nesdělujeme třetím stranám.

Výjimky:

• V případě potřeby - v souladu se zákonem, soudním řízením, soudním řízením a/nebo na základě žádostí veřejnosti nebo žádostí od vládní agentury na území Ruské federace – zveřejněte své osobní údaje. Můžeme také zveřejnit informace o vás, pokud usoudíme, že takové zveřejnění je nezbytné nebo vhodné pro účely bezpečnosti, vymáhání práva nebo jiné veřejné důležité účely.
• V případě reorganizace, fúze nebo prodeje můžeme osobní údaje, které shromažďujeme, předat příslušné nástupnické třetí straně.

Ochrana osobních údajů

Přijímáme opatření – včetně administrativních, technických a fyzických – k ochraně vašich osobních údajů před ztrátou, krádeží a zneužitím, stejně jako neoprávněným přístupem, zveřejněním, pozměněním a zničením.

Respektování vašeho soukromí na úrovni společnosti

Abychom zajistili, že jsou vaše osobní údaje v bezpečí, sdělujeme našim zaměstnancům standardy ochrany soukromí a zabezpečení a přísně prosazujeme postupy ochrany osobních údajů.

Řešení rovnic a nerovnic s modulemčasto způsobuje potíže. Pokud však dobře chápete, o co jde absolutní hodnota čísla, A jak správně rozbalit výrazy obsahující znaménko modulu, pak přítomnost v rovnici výraz pod znaménkem modulu, přestává být překážkou jeho řešení.

Trochu teorie. Každé číslo má dvě vlastnosti: absolutní hodnotu čísla a jeho znaménko.

Například číslo +5 nebo jednoduše 5 má znaménko „+“ a absolutní hodnotu 5.

Číslo -5 má znaménko "-" a absolutní hodnotu 5.

Absolutní hodnoty čísel 5 a -5 jsou 5.

Absolutní hodnota čísla x se nazývá modul čísla a značí se |x|.

Jak vidíme, modul čísla se rovná samotnému číslu, pokud je toto číslo větší nebo rovno nule, a tomuto číslu s opačným znaménkem, je-li toto číslo záporné.

Totéž platí pro všechny výrazy, které se objeví pod znaménkem modulu.

Pravidlo rozšíření modulu vypadá takto:

|f(x)|= f(x), pokud f(x) ≥ 0, a

|f(x)|= - f(x), pokud f(x)< 0

Například |x-3|=x-3, pokud x-3≥0 a |x-3|=-(x-3)=3-x, pokud x-3<0.

Chcete-li vyřešit rovnici obsahující výraz pod znaménkem modulu, musíte nejprve rozšiřte modul podle pravidla rozšiřování modulu.

Pak se stane naše rovnice nebo nerovnost do dvou různých rovnic existujících na dvou různých číselných intervalech.

Jedna rovnice existuje na číselném intervalu, na kterém je výraz pod znaménkem modulu nezáporný.

A druhá rovnice existuje na intervalu, na kterém je výraz pod znaménkem modulu záporný.

Podívejme se na jednoduchý příklad.

Pojďme řešit rovnici:

|x-3|=-x 2 +4x-3

1. Otevřeme modul.

|x-3|=x-3, pokud x-3≥0, tj. pokud x≥3

|x-3|=-(x-3)=3-x pokud x-3<0, т.е. если х<3

2. Dostali jsme dva číselné intervaly: x≥3 a x<3.

Uvažujme, do kterých rovnic se původní rovnice na každém intervalu transformuje:

A) Pro x≥3 |x-3|=x-3 a naše zranění má tvar:

Pozornost! Tato rovnice existuje pouze na intervalu x≥3!

Otevřeme závorky a představíme podobné pojmy:

a vyřešit tuto rovnici.

Tato rovnice má kořeny:

x 1 = 0, x 2 = 3

Pozornost! protože rovnice x-3=-x 2 +4x-3 existuje pouze na intervalu x≥3, zajímají nás pouze ty kořeny, které do tohoto intervalu patří. Tuto podmínku splňuje pouze x 2 =3.

B) V x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

Pozornost! Tato rovnice existuje pouze na intervalu x<3!

Otevřeme závorky a představíme podobné pojmy. Dostaneme rovnici:

x 1 = 2, x 2 = 3

Pozornost! protože rovnice 3-x=-x 2 +4x-3 existuje pouze na intervalu x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

Takže: z prvního intervalu vezmeme pouze kořen x=3, z druhého - kořen x=2.

Nevybíráme si matematiku její profesi a ona si nás vybírá.

Ruský matematik Yu.I. Manin

Rovnice s modulem

Nejobtížněji řešitelnými problémy ve školní matematice jsou rovnice obsahující proměnné pod znaménkem modulu. Pro úspěšné řešení takových rovnic je potřeba znát definici a základní vlastnosti modulu. Přirozeně, že studenti musí mít dovednosti řešit rovnice tohoto typu.

Základní pojmy a vlastnosti

Modul (absolutní hodnota) reálného čísla označený a je definován takto:

Jednoduché vlastnosti modulu zahrnují následující vztahy:

Poznámka, že poslední dvě vlastnosti platí pro libovolný sudý stupeň.

Navíc když, kde, pak a

Složitější vlastnosti modulu, které lze efektivně využít při řešení rovnic s moduly, jsou formulovány pomocí následujících vět:

Věta 1.Pro jakékoli analytické funkce A nerovnost je pravdivá

Věta 2. Rovnost je ekvivalentní nerovnosti.

Věta 3. Rovnost rovná nerovnosti.

Podívejme se na typické příklady řešení úloh na téma „Rovnice, obsahující proměnné pod znaménkem modulu."

Řešení rovnic s modulem

Nejběžnější metodou ve školní matematice pro řešení rovnic s modulem je metoda, na základě rozšíření modulu. Tato metoda je univerzální, v obecném případě však jeho použití může vést k velmi těžkopádným výpočtům. V tomto ohledu by studenti měli znát jiné, efektivnější metody a techniky pro řešení takových rovnic. Zejména, je nutné mít dovednosti v aplikaci teorémů, uvedeno v tomto článku.

Příklad 1 Vyřešte rovnici. (1)

Řešení. Rovnici (1) budeme řešit „klasickou“ metodou – metodou odhalování modulů. Chcete-li to provést, rozdělme číselnou osu tečky a do intervalů a zvažte tři případy.

1. Jestliže , pak , , a rovnice (1) mají tvar . Z toho vyplývá. Zde však nalezená hodnota není kořenem rovnice (1).

2. Pokud, pak z rovnice (1) dostaneme nebo .

Od té doby kořen rovnice (1).

3. Pokud, pak rovnice (1) nabývá tvaru nebo . Všimněme si toho.

Odpovědět: , .

Při řešení následných rovnic s modulem budeme aktivně využívat vlastnosti modulů, abychom zvýšili efektivitu řešení takových rovnic.

Příklad 2 Vyřešte rovnici.

Řešení. Od a pak z rovnice vyplývá. V tomto kontextu, , , a rovnice má tvar. Odtud se dostáváme. Nicméně , proto původní rovnice nemá kořeny.

Odpověď: žádné kořeny.

Příklad 3 Vyřešte rovnici.

Řešení. Od té doby. Pokud, pak a rovnice má tvar.

Odtud se dostáváme.

Příklad 4. Vyřešte rovnici.

Řešení.Přepišme rovnici do ekvivalentního tvaru. (2)

Výsledná rovnice patří k rovnicím typu .

Vezmeme-li v úvahu větu 2, lze tvrdit, že rovnice (2) je ekvivalentní nerovnosti . Odtud se dostáváme.

Odpovědět: .

Příklad 5. Vyřešte rovnici.

Řešení. Tato rovnice má tvar. Proto , podle věty 3, tady máme nerovnost nebo .

Příklad 6. Vyřešte rovnici.

Řešení. Předpokládejme to. Protože , pak má daná rovnice tvar kvadratické rovnice, (3)

Kde . Protože rovnice (3) má jediný kladný kořen a pak . Odtud dostáváme dva kořeny původní rovnice: A .

Příklad 7. Vyřešte rovnici. (4)

Řešení. Od rovniceje ekvivalentní kombinaci dvou rovnic: A , pak při řešení rovnice (4) je nutné uvažovat dva případy.

1. Pokud , pak nebo .

Odtud dostáváme , a .

2. Pokud , pak nebo .

Od té doby.

Odpovědět: , , , .

Příklad 8.Vyřešte rovnici . (5)

Řešení. Od a poté. Odtud a z rovnice (5) vyplývá, že a , tzn. zde máme soustavu rovnic

Tento systém rovnic je však nekonzistentní.

Odpověď: žádné kořeny.

Příklad 9. Vyřešte rovnici. (6)

Řešení. Pokud označíme , tak a z rovnice (6) dostaneme

Nebo . (7)

Protože rovnice (7) má tvar , je tato rovnice ekvivalentní nerovnosti . Odtud se dostáváme. Od té doby nebo .

Odpovědět: .

Příklad 10.Vyřešte rovnici. (8)

Řešení.Podle věty 1 můžeme psát

(9)

Vezmeme-li v úvahu rovnici (8), docházíme k závěru, že obě nerovnosti (9) přecházejí v rovnosti, tzn. existuje soustava rovnic

Podle věty 3 je však výše uvedená soustava rovnic ekvivalentní soustavě nerovnic

(10)

Řešením soustavy nerovnic (10) získáme . Protože systém nerovnic (10) je ekvivalentní rovnici (8), má původní rovnice jeden kořen.

Odpovědět: .

Příklad 11. Vyřešte rovnici. (11)

Řešení. Nechť a , pak rovnost vyplývá z rovnice (11).

Z toho vyplývá a . Máme zde tedy systém nerovností

Řešením tohoto systému nerovností je A .

Odpovědět: , .

Příklad 12.Vyřešte rovnici. (12)

Řešení. Rovnice (12) bude řešena metodou sekvenčního rozšiřování modulů. Chcete-li to provést, zvažte několik případů.

1. Pokud , pak .

1.1. Pokud , pak a , .

1.2. Pokud, tak. Nicméně , proto v tomto případě rovnice (12) nemá kořeny.

2. Pokud , pak .

2.1. Pokud , pak a , .

2.2. Pokud , pak a .

Odpovědět: , , , , .

Příklad 13.Vyřešte rovnici. (13)

Řešení. Protože levá strana rovnice (13) je nezáporná, pak . V tomto ohledu a rovnice (13)

má podobu nebo .

Je známo, že rovnice je ekvivalentní kombinaci dvou rovnic A , řešení, které dostaneme, . Protože , pak rovnice (13) má jeden kořen.

Odpovědět: .

Příklad 14. Řešte soustavu rovnic (14)

Řešení. Od a , potom a . V důsledku toho ze soustavy rovnic (14) získáme čtyři soustavy rovnic:

Kořeny výše uvedených soustav rovnic jsou kořeny soustavy rovnic (14).

Odpovědět: ,, , , , , , .

Příklad 15. Řešte soustavu rovnic (15)

Řešení. Od té doby. V tomto ohledu ze soustavy rovnic (15) dostáváme dvě soustavy rovnic

Kořeny první soustavy rovnic jsou a , a z druhé soustavy rovnic získáme a .

Odpovědět: , , , .

Příklad 16. Řešte soustavu rovnic (16)

Řešení. Z první rovnice soustavy (16) vyplývá, že .

Od té doby . Uvažujme druhou rovnici soustavy. Protože, Že , a rovnice má tvar, , nebo .

Pokud dosadíte hodnotudo první rovnice soustavy (16), pak , nebo .

Odpovědět: , .

Pro hlubší studium metod řešení problémů, související s řešením rovnic, obsahující proměnné pod znaménkem modulu, Výukové programy můžete doporučit ze seznamu doporučené literatury.

1. Sbírka úloh z matematiky pro uchazeče na vysoké školy / Ed. M.I. Scanavi. – M.: Mír a vzdělání, 2013. – 608 s.

2. Suprun V.P. Matematika pro středoškoláky: úlohy se zvýšenou složitostí. – M.: CD „Librocom“ / URSS, 2017. – 200 s.

3. Suprun V.P. Matematika pro středoškoláky: nestandardní metody řešení úloh. – M.: CD „Librocom“ / URSS, 2017. – 296 s.

Máte ještě otázky?

Chcete-li získat pomoc od lektora, zaregistrujte se.

webové stránky, při kopírování celého materiálu nebo jeho části je vyžadován odkaz na zdroj.

Střední škola MBOU č. 17, Ivanovo

« Rovnice s modulem"
Metodický vývoj

Sestaven

učitel matematiky

Lebedeva N.V.

20010

Vysvětlivka

Kapitola 1 Úvod

Sekce 2. Základní vlastnosti Oddíl 3. Geometrická interpretace pojmu modul čísla Sekce 4. Graf funkce y = |x| Oddíl 5. Úmluvy

Kapitola 2. Řešení rovnic obsahujících modul

Oddíl 1. Rovnice tvaru |F(x)| = m (nejjednodušší) Oddíl 2. Rovnice tvaru F(|x|) = m Oddíl 3. Rovnice tvaru |F(x)| = G(x) Oddíl 4. Rovnice tvaru |F(x)| = ± F(x) (nejkrásnější) Oddíl 5. Rovnice tvaru |F(x)| = |G(x)| Sekce 6. Příklady řešení nestandardních rovnic Oddíl 7. Rovnice tvaru |F(x)| + |G(x)| = 0 Oddíl 8. Rovnice tvaru |a 1 x ± b 1 | ± |a 2 x ± ve 2 | ± …|a n x ± v n | = m Oddíl 9. Rovnice obsahující několik modulů

Kapitola 3. Příklady řešení různých rovnic s modulem.

Sekce 1. Goniometrické rovnice Sekce 2. Exponenciální rovnice Oddíl 3. Logaritmické rovnice Oddíl 4. Iracionální rovnice Sekce 5. Pokročilé úkoly Odpovědi na cvičení Bibliografie

Vysvětlivka.

Pojem absolutní hodnoty (modulu) reálného čísla je jednou z jeho podstatných vlastností. Tento koncept má široké využití v různých úsecích fyzikálních, matematických a technických věd. V praxi výuky matematických kurzů na středních školách v souladu s Programem Ministerstva obrany Ruské federace se s pojmem „absolutní hodnota čísla“ setkáváme opakovaně: v 6. ročníku je definována definice modulu resp. je představen jeho geometrický význam; v 8. ročníku se tvoří pojem absolutní chyba, uvažuje se o řešení nejjednodušších rovnic a nerovnic obsahujících modul a studují se vlastnosti aritmetické odmocniny; v 11. třídě se koncept nachází v sekci „Root n- stupeň." Zkušenosti z výuky ukazují, že studenti se často setkávají s obtížemi při řešení úloh, které vyžadují znalost této látky, a často je přeskakují, aniž by je začali plnit. Podobná zadání obsahují i ​​texty zadání zkoušek pro předměty 9. a 11. ročníku. Požadavky, které vysoké školy kladou na absolventy škol, jsou navíc jiné, a to na vyšší úrovni než požadavky školního vzdělávacího programu. Pro život v moderní společnosti je velmi důležité formování matematického stylu myšlení, projevujícího se v určitých mentálních dovednostech. V procesu řešení problémů s moduly je vyžadována schopnost používat techniky, jako je zobecnění a specifikace, analýza, klasifikace a systematizace a analogie. Řešení takových úkolů vám umožní otestovat své znalosti hlavních částí školního kurzu, úroveň logického myšlení a počáteční výzkumné dovednosti. Tato práce je věnována jedné z sekcí - řešení rovnic obsahující modul. Skládá se ze tří kapitol. První kapitola uvádí základní pojmy a nejdůležitější teoretické úvahy. Druhá kapitola navrhuje devět hlavních typů rovnic obsahujících modul, probírá metody jejich řešení a zkoumá příklady různých úrovní složitosti. Třetí kapitola nabízí složitější a nestandardní rovnice (trigonometrické, exponenciální, logaritmické a iracionální). Pro každý typ rovnic jsou cvičení pro samostatné řešení (odpovědi a návod jsou přiloženy). Hlavním účelem této práce je poskytnout metodickou pomoc učitelům při přípravě na vyučování a při organizaci volitelných předmětů. Materiál lze využít i jako učební pomůcku pro středoškoláky. Úkoly navržené v práci jsou zajímavé a ne vždy snadno řešitelné, což umožňuje více uvědomovat si vzdělávací motivaci studentů, testovat jejich schopnosti a zvyšovat úroveň přípravy absolventů škol na vstup na vysoké školy. Diferencovaný výběr navrhovaných cvičení zahrnuje přechod z reprodukční úrovně zvládnutí materiálu na kreativní a také příležitost naučit se aplikovat své znalosti při řešení nestandardních problémů.

Kapitola 1 Úvod.

Oddíl 1. Stanovení absolutní hodnoty .

Definice : Absolutní hodnota (modul) reálného čísla A nezáporné číslo se nazývá: A nebo -A. Označení: │ A │ Záznam zní takto: „modul čísla a“ nebo „absolutní hodnota čísla a“

│ a, pokud a > 0

│a│ = │ 0, pokud a = 0 (1)

│ - a pokud a
Příklady: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Rozbalit modul výrazu:

a) │x - 8│, pokud x > 12 b) │2x + 3│, pokud x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Sekce 2. Základní vlastnosti.

Uvažujme základní vlastnosti absolutní hodnoty. Vlastnost č. 1: Opačná čísla mají stejné moduly, tzn. │а│=│- а│ Ukažme, že rovnost je pravdivá. Zapišme si definici čísla - A : │- a│= (2) Porovnejme množiny (1) a (2). Je zřejmé, že definice absolutních hodnot čísel A A - A sladit se. Proto, │а│=│- а│
Při zvažování následujících vlastností se omezíme na jejich formulaci, protože jejich důkaz je uveden v Vlastnost č. 2: Absolutní hodnota součtu konečného počtu reálných čísel nepřesahuje součet absolutních hodnot členů: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Vlastnost č. 3: Absolutní hodnota rozdílu dvou reálných čísel nepřesahuje součet jejich absolutních hodnot: │а - в│ ≤│а│+│в│ Vlastnost č. 4: Absolutní hodnota součinu konečného počtu reálných čísel se rovná součinu absolutních hodnot faktorů: │а·в│=│а│·│в│ Vlastnost č. 5: Absolutní hodnota podílu reálných čísel se rovná podílu jejich absolutních hodnot:

Oddíl 3. Geometrický výklad pojmu modul čísla.

Každé reálné číslo může být spojeno s bodem na číselné ose, který bude geometrickým obrazem tohoto reálného čísla. Každému bodu na číselné ose odpovídá jeho vzdálenost od počátku, tzn. délka segmentu od počátku k danému bodu. Tato vzdálenost je vždy považována za nezápornou hodnotu. Proto délka odpovídajícího segmentu bude geometrickou interpretací absolutní hodnoty daného reálného čísla

Předložená geometrická ilustrace jednoznačně potvrzuje vlastnost č. 1, tzn. moduly opačných čísel jsou stejné. Odtud lze snadno pochopit platnost rovnosti: │х – а│= │а – x│. Řešení rovnice │х│= m, kde m ≥ 0, konkrétně x 1,2 = ± m, se také stává zjevnějším. Příklady: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

Sekce 4. Graf funkce y = │х│

Definičním oborem této funkce jsou všechna reálná čísla.

Oddíl 5. Úmluvy.

V budoucnu se při zvažování příkladů řešení rovnic budou používat následující konvence: ( - znak systému [ - znak totality Při řešení soustavy rovnic (nerovnic) je nalezen průnik řešení rovnic (nerovnic) obsažených v soustavě. Při řešení soustavy rovnic (nerovnic) se nalézá sjednocení řešení obsažených v soustavě rovnic (nerovnic).

Kapitola 2. Řešení rovnic obsahujících modul.

V této kapitole se podíváme na algebraické metody řešení rovnic obsahujících jeden nebo více modulů.

Oddíl 1. Rovnice ve tvaru │F (x)│= m

Rovnice tohoto typu se nazývá nejjednodušší. Má řešení právě tehdy, když m ≥ 0. Podle definice modulu je původní rovnice ekvivalentní soustavě dvou rovnic: │ F(x)│=m
Příklady:
№1. Vyřešte rovnici: │7х - 2│= 9


Odpověď: x 1 = -1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Odpověď: součet kořenů je - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 značí x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5 m + 4 = 0 m = 1; 4 – obě hodnoty splňují podmínku m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Odpověď: počet kořenů rovnice 7. Cvičení:
№1. Vyřešte rovnici a uveďte součet kořenů: │х - 5│= 3 №2 . Vyřešte rovnici a označte menší kořen: │x 2 + x│= 0 №3 . Vyřešte rovnici a označte větší odmocninu: │x 2 – 5x + 4│= 4 №4 .Vyřešte rovnici a označte celý kořen: │2x 2 – 7x + 6│= 1 №5 .Vyřešte rovnici a uveďte počet kořenů: │x 4 – 13x 2 + 50│= 14

Oddíl 2. Rovnice tvaru F(│х│) = m

Argument funkce na levé straně je pod znaménkem modulu a pravá strana je nezávislá na proměnné. Uvažujme dva způsoby řešení rovnic tohoto typu. 1 způsob: Podle definice absolutní hodnoty je původní rovnice ekvivalentní kombinaci dvou systémů. V každém z nich je podmínka uložena na submodulární výraz. F(│х│) =m
Protože funkce F(│x│) je sudá v celém definičním oboru, kořeny rovnic F(x) = m a F(- x) = m jsou dvojice opačných čísel. Stačí tedy vyřešit jeden ze systémů (při zvažování příkladů tímto způsobem bude uvedeno řešení jednoho systému). Metoda 2: Aplikace metody zavedení nové proměnné. V tomto případě se zavádí označení │x│= a, kde a ≥ 0. Tato metoda je designově méně objemná.
Příklady: №1 . Vyřešte rovnici: 3x 2 – 4│x│= - 1 Použijme zavedení nové proměnné. Označme │x│= a, kde a ≥ 0. Získáme rovnici 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Návrat k původní proměnné: │ x│=1 a │х│= 1/3. Každá rovnice má dva kořeny. Odpověď: x 1 = 1; X 2 = -1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Vyřešte rovnici: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
Pojďme najít řešení pro první systém populace: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Všimněte si, že x 2 nevyhovuje podmínka x ≥ 0. Řešení druhá soustava bude číslo opačné k hodnotě x 1. Odpověď: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Řešte rovnici: x 4 – │х│= 0 Označme │х│= a, kde a ≥ 0. Dostaneme rovnici a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Návrat k původní proměnné: │х│=0 a │х│= 1 x = 0; ± 1 Odpověď: x 1 = 0; X 2 = 1; X 3 = - 1.
Cvičení: №6. Vyřešte rovnici: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Vyřešte rovnici, uveďte počet kořenů ve své odpovědi: 3x 2 - 7│x│ + 2 = 0 №8 . Vyřešte rovnici, uveďte v odpovědi celočíselná řešení: x 4 + │x│ - 2 = 0

Oddíl 3. Rovnice tvaru │F(x)│ = G(x)

Pravá strana rovnice tohoto typu závisí na proměnné, a proto má řešení právě tehdy, když je pravá strana funkcí G(x) ≥ 0. Původní rovnici lze vyřešit dvěma způsoby : 1 způsob: Standard, založený na zveřejnění modulu na základě jeho definice a sestává z ekvivalentního přechodu na kombinaci dvou systémů. │ F(x)│ =G(X)

Tuto metodu lze racionálně použít v případě komplexního výrazu pro funkci G(x) a méně komplexního pro funkci F(x), protože se předpokládá, že se budou řešit nerovnosti s funkcí F(x). Metoda 2: Spočívá v přechodu na ekvivalentní systém, ve kterém je na pravé straně uložena podmínka. │ F(X)│= G(X)

Tuto metodu je vhodnější použít, pokud je výraz pro funkci G(x) méně komplexní než pro funkci F(x), protože se předpokládá řešení nerovnosti G(x) ≥ 0 v případě z několika modulů se doporučuje použít druhou možnost. Příklady: №1. Řešte rovnici: │x + 2│= 6 -2x
(1 cesta) Odpověď: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(2 cesty) Odpověď: Součin kořenů je 3.
№3. Vyřešte rovnici a uveďte součet kořenů ve své odpovědi:
│x - 6│= x 2 - 5x + 9

Odpověď: součet kořenů je 4.
Cvičení: №9. │x + 4│= - 3x №10. Vyřešte rovnici, uveďte počet řešení ve své odpovědi:│x 2 + x - 1│= 2x – 1 №11 . Vyřešte rovnici, uveďte součin odmocnin ve své odpovědi:│x + 3│= x 2 + x – 6

Oddíl 4. Rovnice tvaru │F(x)│= F(x) a │F(x)│= - F(x)

Rovnice tohoto typu se někdy nazývají „nejkrásnější“. Protože pravá strana rovnic závisí na proměnné, řešení existují právě tehdy, když je pravá strana nezáporná. Proto jsou původní rovnice ekvivalentní nerovnostem:
│F(x)│= F(x) F(x) ≥ 0 a │F(x)│= - F(x) F(x) Příklady: №1 . Vyřešte rovnici, uveďte menší odmocninu celého čísla ve své odpovědi: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Odpověď: x = 1№2. Vyřešte rovnici, uveďte v odpovědi délku intervalu: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Odpověď: délka mezery je 6.№3 . Vyřešte rovnici a uveďte počet celočíselných řešení ve své odpovědi: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Odpověď: 4 celá řešení.№4 . Vyřešte rovnici a označte největší kořen ve své odpovědi:
│4 – x –
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Odpověď: x = 3.

Cvičení: №12. Vyřešte rovnici, uveďte v odpovědi celý kořen: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Vyřešte rovnici, uveďte počet celočíselných řešení ve své odpovědi: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Vyřešte rovnici ve své odpovědi uveďte celé číslo, které není kořenem rovnice:

Oddíl 5. Rovnice tvaru │F(x)│= │G(x)│

Protože obě strany rovnice jsou nezáporné, řešení zahrnuje uvažování dvou případů: submodulární výrazy jsou stejné nebo opačné ve znaménku. Původní rovnice je tedy ekvivalentní kombinaci dvou rovnic: │ F(X)│= │ G(X)│
Příklady: №1. Vyřešte rovnici, uveďte v odpovědi celý kořen: │x + 3│=│2x - 1│
Odpověď: celý kořen x = 4.№2. Řešte rovnici: │ x – x 2 – 1│=│2x – 3 – x 2 │
Odpověď: x = 2.№3 . Vyřešte rovnici a uveďte součin kořenů ve své odpovědi:




Kořenové rovnice 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Odpověď: součin kořenů je – 0,25. Cvičení: №15 . Vyřešte rovnici a uveďte celé řešení ve své odpovědi: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Vyřešte rovnici, označte menší odmocninu ve své odpovědi:│5x - 3│=│7 - x│ №17 . Vyřešte rovnici a uveďte součet kořenů ve své odpovědi:

Sekce 6. Příklady řešení nestandardních rovnic

V této části se podíváme na příklady nestandardních rovnic, při jejichž řešení je z definice odhalena absolutní hodnota výrazu. Příklady:

№1. Vyřešte rovnici, uveďte součet kořenů ve své odpovědi: x · │x│- 5x – 6 = 0
Odpověď: součet kořenů je 1 №2. . Vyřešte rovnici, označte menší odmocninu ve své odpovědi: x 2 - 4x ·
- 5 = 0
Odpověď: menší odmocnina x = - 5. №3. Řešte rovnici:

Odpověď: x = -1. Cvičení: №18. Vyřešte rovnici a uveďte součet odmocnin: x · │3x + 5│= 3x 2 + 4x + 3
№19. Řešte rovnici: x 2 – 3x =

№20. Řešte rovnici:

Oddíl 7. Rovnice tvaru │F(x)│+│G(x)│=0

Je snadné si všimnout, že na levé straně rovnice tohoto typu je součet nezáporných veličin. Původní rovnice má tedy řešení právě tehdy, když jsou oba členy ve stejnou dobu rovny nule. Rovnice je ekvivalentní soustavě rovnic: │ F(X)│+│ G(X)│=0
Příklady: №1 . Řešte rovnici:
Odpověď: x = 2. №2. Řešte rovnici: Odpověď: x = 1. Cvičení: №21. Řešte rovnici: №22 . Vyřešte rovnici a uveďte součet kořenů ve své odpovědi: №23 . Vyřešte rovnici a uveďte počet řešení ve své odpovědi:

Oddíl 8. Rovnice tvaru │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

K řešení rovnic tohoto typu se používá intervalová metoda. Pokud to vyřešíme sekvenčním rozšiřováním modulů, dostaneme n sady systémů, což je velmi těžkopádné a nepohodlné. Uvažujme algoritmus intervalové metody: 1). Najděte hodnoty proměnných X, pro které je každý modul roven nule (nuly submodulárních výrazů):
2). Nalezené hodnoty označte na číselné ose, která je rozdělena do intervalů (počet intervalů je roven n+1 ) 3). Určete, jakým znaménkem je každý modul odhalen v každém ze získaných intervalů (při řešení můžete použít číselnou řadu, na ní označující znaménka) 4). Původní rovnice je ekvivalentní agregátu n+1 systémů, v každém z nich je uvedeno členství proměnné X jeden z intervalů. Příklady: №1 . Vyřešte rovnici a označte největší kořen ve své odpovědi:
1). Najděte nuly submodulárních výrazů: x = 2; x = -3 2). Označme nalezené hodnoty na číselné ose a určeme, jakým znaménkem je každý modul odhalen na výsledných intervalech:
x – 2 x – 2 x – 2 – – + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- bez řešení Rovnice má dva kořeny. Odpověď: největší kořen x = 2. №2. Vyřešte rovnici a ve své odpovědi uveďte celý kořen:
1). Najděte nuly submodulárních výrazů: x = 1,5; x = -12). Nalezené hodnoty označme na číselné ose a určeme, jakým znaménkem je každý modul odhalen na výsledných intervalech: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Poslední systém nemá řešení, proto má rovnice dva kořeny. Při řešení rovnice byste měli věnovat pozornost znaménku „-“ před druhým modulem. Odpověď: celý kořen x = 7. №3. Vyřešte rovnici, uveďte součet kořenů ve své odpovědi: 1). Najděte nuly submodulárních výrazů: x = 5; x = 1; x = -22). Nalezené hodnoty označíme na číselné ose a určíme, jakým znaménkem je každý modul odhalen ve výsledných intervalech: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Rovnice má dva kořeny x = 0 a 2. Odpověď: součet kořenů je 2. №4 . Řešte rovnici: 1). Najděte nuly submodulárních výrazů: x = 1; x = 2; x = 3,2). Pojďme určit, jakým znaménkem je každý modul odhalen na výsledných intervalech. 3).
Spojme řešení prvních tří systémů. Odpovědět: ; x = 5.
Cvičení: №24. Řešte rovnici:
№25. Vyřešte rovnici a uveďte součet kořenů ve své odpovědi: №26. Vyřešte rovnici a ve své odpovědi označte menší odmocninu: №27. Vyřešte rovnici a označte ve své odpovědi větší odmocninu:

Oddíl 9. Rovnice obsahující několik modulů

Rovnice obsahující více modulů předpokládají přítomnost absolutních hodnot v submodulárních výrazech. Základním principem řešení rovnic tohoto typu je postupné zveřejňování modulů, počínaje „vnějším“. Při řešení jsou použity techniky popsané v oddílech č. 1, č. 3.

Příklady: №1. Řešte rovnici:
Odpověď: x = 1; - jedenáct. №2. Řešte rovnici:
Odpověď: x = 0; 4; - 4. №3. Vyřešte rovnici a uveďte součin kořenů ve své odpovědi:
Odpověď: součin kořenů je – 8. №4. Řešte rovnici:
Označme rovnice populace (1) A (2) a zvážit řešení každého z nich zvlášť pro usnadnění návrhu. Protože obě rovnice obsahují více než jeden modul, je vhodnější provést ekvivalentní přechod na množiny systémů. (1)

(2)


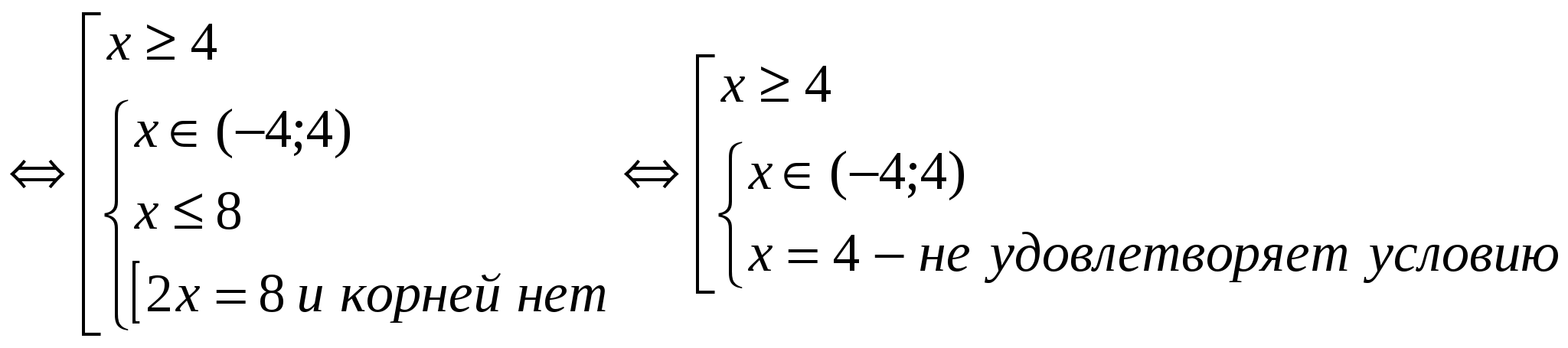Odpovědět:
Cvičení: №36. Vyřešte rovnici, uveďte součet kořenů ve své odpovědi: 5 │3x-5│ = 25 x №37. Vyřešte rovnici, pokud existuje více než jeden kořen, uveďte ve své odpovědi součet kořenů: │x + 2│ x – 3x – 10 = 1 №38. Vyřešte rovnici: 3 │2х -4│ = 9 │х│ №39. Vyřešte rovnici, ve své odpovědi uveďte počet kořenů na: 2 │ sin x│ = √2 №40 . Vyřešte rovnici a uveďte počet kořenů ve své odpovědi:

Oddíl 3. Logaritmické rovnice.

Před řešením následujících rovnic je nutné zopakovat vlastnosti logaritmů a logaritmické funkce. Příklady: №1. Vyřešte rovnici, uveďte součin kořenů ve své odpovědi: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Případ 1: pokud x ≥ - 1, pak log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – splňuje podmínku x ≥ - 1 2 případ: pokud x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – splňuje podmínku x - 1
Odpověď: součin kořenů je – 15.
№2. Vyřešte rovnici, uveďte součet kořenů ve své odpovědi: lg
O.D.Z.

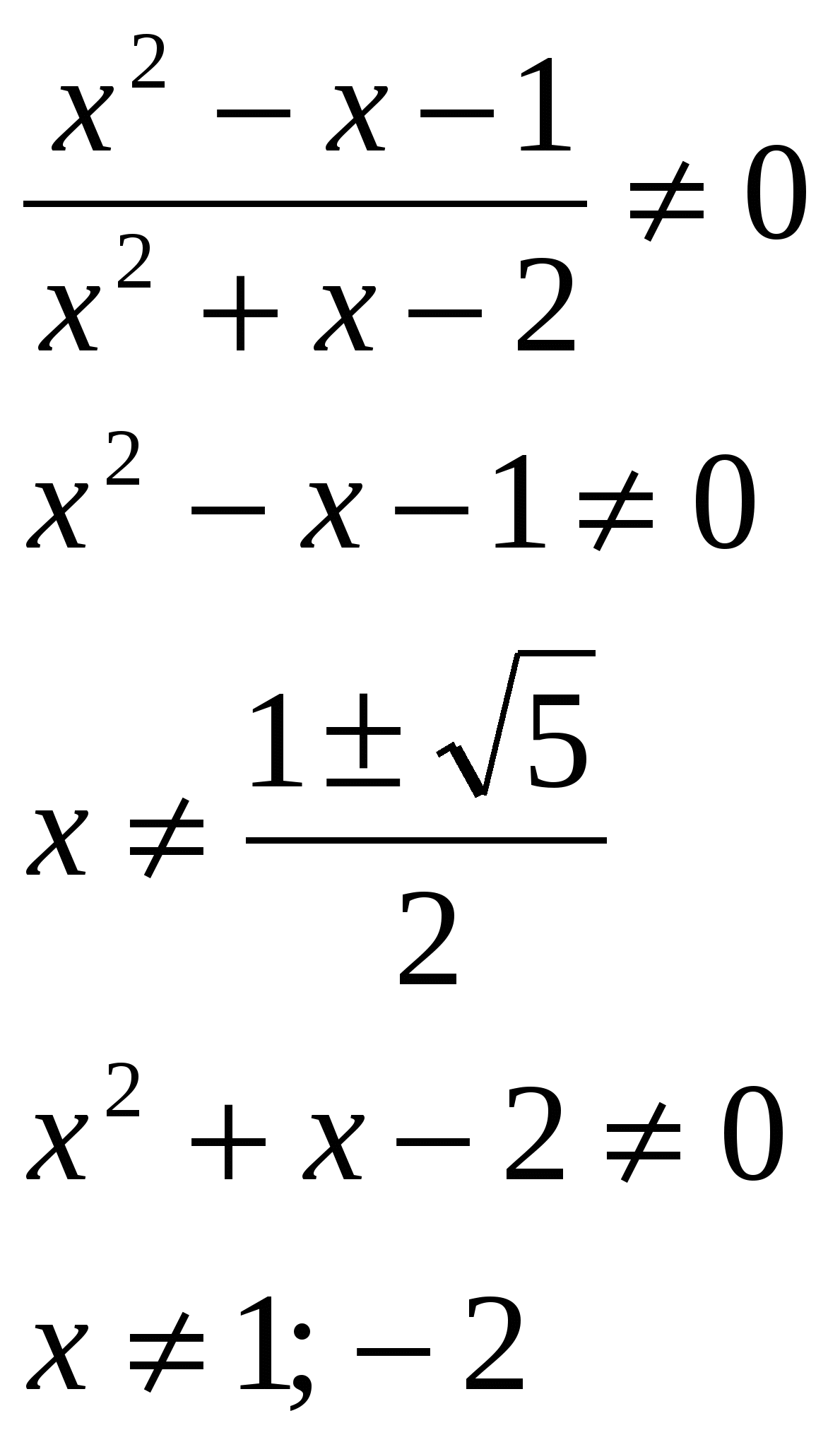
Odpověď: součet kořenů je 0,5.
№3. Řešte rovnici: log 5
O.D.Z.

Odpověď: x = 9. №4. Řešte rovnici: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Použijme vzorec pro přesun na jiný základ. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Najdeme nuly submodulárních výrazů: x = 25; x = Tato čísla rozdělují rozsah přijatelných hodnot do tří intervalů, takže rovnice je ekvivalentní sadě tří systémů.
Odpovědět: )