หาโมดูลัสของผลิตภัณฑ์เวกเตอร์ ผลิตภัณฑ์เวกเตอร์ - คำจำกัดความ คุณสมบัติ สูตร ตัวอย่าง และคำตอบ การดำเนินการเชิงเส้นบนเวกเตอร์

ผลิตภัณฑ์ผสมของเวกเตอร์สามตัวและคุณสมบัติของมัน

งานผสมเวกเตอร์สามตัวเรียกว่าตัวเลขเท่ากับ กำหนด - ตรงนี้ เวกเตอร์สองตัวแรกจะถูกคูณด้วยเวกเตอร์ จากนั้นเวกเตอร์ที่ได้จะถูกคูณด้วยเวกเตอร์ตัวที่สามแบบสเกลาร์ แน่นอนว่าผลิตภัณฑ์ดังกล่าวมีจำนวนที่แน่นอน

พิจารณาคุณสมบัติของผลิตภัณฑ์ผสม

1. ความหมายทางเรขาคณิตงานผสม ผลคูณผสมของเวกเตอร์ 3 ตัวจนถึงเครื่องหมายเท่ากับปริมาตรของเส้นขนานที่สร้างขึ้นบนเวกเตอร์เหล่านี้เช่นเดียวกับที่ขอบเช่น -

   ดังนั้นและ .

   

   การพิสูจน์- ลองแยกเวกเตอร์ออกจากกัน จุดเริ่มต้นทั่วไปและสร้างทางขนานไว้บนนั้น ให้เราแสดงและสังเกตว่า . ตามคำจำกัดความของผลิตภัณฑ์สเกลาร์

   สมมติว่าและแสดงถึงโดย ชม.จงหาความสูงของด้านขนาน

   ดังนั้นเมื่อ

   ถ้าเป็นเช่นนั้น เพราะฉะนั้น, .

   เมื่อรวมทั้งสองกรณีนี้เข้าด้วยกัน เราจะได้ หรือ

   จากการพิสูจน์คุณสมบัตินี้ โดยเฉพาะอย่างยิ่ง จะตามมาว่าหากเวกเตอร์สามตัวเป็นแบบถนัดขวา ผลคูณผสมจะเป็น และหากเป็นแบบถนัดซ้าย แล้ว

2. สำหรับเวกเตอร์ใดๆ , , ความเท่าเทียมกันเป็นจริง

   หลักฐานของทรัพย์สินนี้ตามมาจากทรัพย์สินที่ 1 แท้จริงแล้วเป็นการแสดงให้เห็นได้ง่าย และ ยิ่งไปกว่านั้น เครื่องหมาย “+” และ “–” จะถูกถ่ายพร้อมกันเพราะว่า มุมระหว่างเวกเตอร์ และ และ และ มีทั้งมุมแหลมและมุมป้าน

3. เมื่อจัดเรียงปัจจัยทั้งสองใหม่ งานผสมเครื่องหมายการเปลี่ยนแปลง

   แท้จริงแล้วหากเราพิจารณาผลิตภัณฑ์แบบผสมก็เช่นหรือ

4. ผลคูณผสมก็ต่อเมื่อปัจจัยตัวใดตัวหนึ่งมีค่าเท่ากับศูนย์หรือเวกเตอร์เป็นระนาบเดียวกัน

   การพิสูจน์.

   ดังนั้น เงื่อนไขที่จำเป็นและเพียงพอสำหรับ coplanarity ของเวกเตอร์ 3 ตัวก็คือ ผลคูณของเวกเตอร์นั้นมีค่าเท่ากับศูนย์ นอกจากนี้ จะเป็นไปตามนั้นด้วยเวกเตอร์สามตัวที่สร้างพื้นฐานในอวกาศ ถ้า

   หากให้เวกเตอร์อยู่ในรูปแบบพิกัด แสดงว่าสูตรพบผลคูณผสมของเวกเตอร์:

   .

   ดังนั้น ผลคูณผสมจึงเท่ากับดีเทอร์มิแนนต์ลำดับที่สาม ซึ่งมีพิกัดของเวกเตอร์แรกในบรรทัดแรก พิกัดของเวกเตอร์ที่สองในบรรทัดที่สอง และพิกัดของเวกเตอร์ที่สามในบรรทัดที่สาม

   ตัวอย่าง.

เรขาคณิตเชิงวิเคราะห์ในอวกาศ

สมการ ฉ(x, y, z)= 0 กำหนดในช่องว่าง อ็อกซิซพื้นผิวบางส่วน เช่น สถานทางเรขาคณิตของจุดที่มีพิกัด x, y, zเป็นไปตามสมการนี้ สมการนี้เรียกว่าสมการพื้นผิว และ x, y, z– พิกัดปัจจุบัน

อย่างไรก็ตาม บ่อยครั้งที่พื้นผิวไม่ได้ระบุด้วยสมการ แต่เป็นเซตของจุดในอวกาศที่มีคุณสมบัติอย่างใดอย่างหนึ่ง ในกรณีนี้ จำเป็นต้องค้นหาสมการของพื้นผิวตามคุณสมบัติทางเรขาคณิต

เครื่องบิน.

เวกเตอร์เครื่องบินปกติ

สมการของเครื่องบินที่ผ่านจุดที่กำหนด

ให้เราพิจารณาระนาบใดก็ได้ σ ในอวกาศ ตำแหน่งถูกกำหนดโดยการระบุเวกเตอร์ที่ตั้งฉากกับระนาบนี้และจุดคงที่บางจุด M0(x 0, ใช่ 0, ซี 0) นอนอยู่ในระนาบ σ

เวกเตอร์ ตั้งฉากกับเครื่องบินσ เรียกว่า ปกติเวกเตอร์ของเครื่องบินลำนี้ ให้เวกเตอร์มีพิกัด

ลองหาสมการของระนาบ σ ที่ผ่านจุดนี้มา M0และมีเวกเตอร์ตั้งฉาก เมื่อต้องการทำเช่นนี้ ให้ใช้จุดใดก็ได้บนระนาบ σ ม(x, ย, z)และพิจารณาเวกเตอร์

ไม่ว่าจะจุดไหนก็ตาม มО σ เป็นเวกเตอร์ ดังนั้น ผลคูณสเกลาร์ของพวกมันจึงเท่ากับศูนย์ ความเท่าเทียมกันนี้คือเงื่อนไขที่จุด มโอซิ. ใช้ได้กับทุกจุดของระนาบนี้และถูกละเมิดทันทีที่จุดนั้น มจะอยู่นอกระนาบ σ

ถ้าเราแทนจุดด้วยเวกเตอร์รัศมี ม, – เวกเตอร์รัศมีของจุด M0จึงสามารถเขียนสมการได้ในรูป

สมการนี้เรียกว่า เวกเตอร์สมการระนาบ ลองเขียนมันในรูปแบบพิกัดกัน ตั้งแต่นั้นเป็นต้นมา

เราก็ได้สมการของระนาบที่ผ่านจุดนี้มา ดังนั้น เพื่อสร้างสมการของระนาบ คุณจำเป็นต้องทราบพิกัดของเวกเตอร์ปกติและพิกัดของจุดใดจุดหนึ่งที่วางอยู่บนระนาบ

โปรดทราบว่าสมการของระนาบคือสมการระดับที่ 1 เทียบกับพิกัดปัจจุบัน เอ็กซ์, ยและ z.

ตัวอย่าง.

สมการทั่วไปของเครื่องบิน

จะเห็นได้ว่าสมการดีกรีหนึ่งใดๆ เทียบกับพิกัดคาร์ทีเซียน x, y, zแสดงถึงสมการของระนาบที่แน่นอน สมการนี้เขียนเป็น:

ขวาน+โดย+Cz+D=0

และถูกเรียกว่า สมการทั่วไประนาบและพิกัด ก, บี, ซีนี่คือพิกัดของเวกเตอร์ปกติของเครื่องบิน

ให้เราพิจารณากรณีพิเศษของสมการทั่วไป เรามาดูกันว่าระนาบนั้นสัมพันธ์กับระบบพิกัดอย่างไรหากค่าสัมประสิทธิ์ของสมการตั้งแต่หนึ่งค่าขึ้นไปกลายเป็นศูนย์

A คือความยาวของส่วนที่ตัดออกโดยระนาบบนแกน วัว- ในทำนองเดียวกันก็สามารถแสดงให้เห็นได้ว่า ขและ ค– ความยาวของปล้องที่เครื่องบินตัดออกโดยคำนึงถึงแกน เฮ้ยและ ออนซ์.

สะดวกในการใช้สมการของระนาบในส่วนต่างๆ เพื่อสร้างระนาบ

แน่นอน ในกรณีของผลิตภัณฑ์เวกเตอร์ ลำดับการใช้เวกเตอร์มีความสำคัญ ยิ่งไปกว่านั้น

นอกจากนี้ โดยตรงจากคำจำกัดความ จะตามมาด้วยว่าสำหรับตัวประกอบสเกลาร์ k (ตัวเลข) ต่อไปนี้จะเป็นจริง:

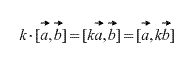
งานศิลปะของเว็กเตอร์เวกเตอร์คอลลิเนียร์เท่ากับเวกเตอร์ศูนย์ ยิ่งไปกว่านั้น ผลคูณไขว้ของเวกเตอร์สองตัวจะเป็นศูนย์ก็ต่อเมื่อพวกมันเป็นเส้นตรงเท่านั้น (ในกรณีที่หนึ่งในนั้นเป็นเวกเตอร์ศูนย์ จำเป็นต้องจำไว้ว่าเวกเตอร์ศูนย์นั้นอยู่ในแนวเดียวกันกับเวกเตอร์ใดๆ ตามคำจำกัดความ)

ผลิตภัณฑ์เวกเตอร์มี ทรัพย์สินจำหน่ายนั่นคือ

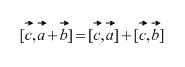
การแสดงผลคูณเวกเตอร์ผ่านพิกัดของเวกเตอร์

ให้เวกเตอร์สองตัวมา

(วิธีค้นหาพิกัดของเวกเตอร์จากพิกัดของจุดเริ่มต้นและจุดสิ้นสุด - ดูบทความ Dot product of vector, item คำจำกัดความทางเลือกของ dot product หรือการคำนวณ dot product ของเวกเตอร์สองตัวที่ระบุโดยพิกัด)

ทำไมคุณถึงต้องการผลิตภัณฑ์เวกเตอร์?

มีหลายวิธีในการใช้ผลคูณไขว้ของเวกเตอร์สองตัว ตามที่เขียนไว้ข้างต้น โดยการคำนวณผลคูณไขว้ของเวกเตอร์สองตัว คุณจะทราบได้ว่าพวกมันอยู่ในแนวเดียวกันหรือไม่

หรือสามารถใช้เป็นวิธีคำนวณพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างจากเวกเตอร์เหล่านี้ได้ ตามคำนิยามความยาวของเวกเตอร์ที่ได้คือพื้นที่ของสี่เหลี่ยมด้านขนานที่กำหนด

นอกจากนี้ยังมีการใช้งานด้านไฟฟ้าและแม่เหล็กเป็นจำนวนมาก

เครื่องคิดเลขผลิตภัณฑ์เวกเตอร์ออนไลน์

หากต้องการค้นหาผลคูณสเกลาร์ของเวกเตอร์สองตัวโดยใช้เครื่องคิดเลขนี้ คุณต้องป้อนในบรรทัดแรกตามลำดับพิกัดของเวกเตอร์แรก ใน วินาที - วินาที- พิกัดของเวกเตอร์สามารถคำนวณได้จากพิกัดของจุดเริ่มต้นและจุดสิ้นสุด (ดูบทความ ผลคูณดอทของเวกเตอร์ รายการ คำจำกัดความอื่นของผลิตภัณฑ์ดอท หรือการคำนวณผลคูณดอทของเวกเตอร์สองตัวที่กำหนดโดยพิกัดของพวกมัน)

คำนิยาม. ผลคูณเวกเตอร์ของเวกเตอร์ a (ตัวคูณ) และเวกเตอร์ที่ไม่ใช่คอลลิเนียร์ (ตัวคูณ) คือเวกเตอร์ตัวที่สาม c (ผลคูณ) ซึ่งสร้างได้ดังนี้:

1) โมดูลัสของมันคือตัวเลข เท่ากับพื้นที่สี่เหลี่ยมด้านขนานในรูป 155) สร้างบนเวกเตอร์ กล่าวคือ เท่ากับทิศทางที่ตั้งฉากกับระนาบของสี่เหลี่ยมด้านขนานดังกล่าว

3) ในกรณีนี้ ทิศทางของเวกเตอร์ c ถูกเลือก (จากสองทิศทางที่เป็นไปได้) เพื่อให้เวกเตอร์ c สร้างระบบทางขวา (§ 110)

การกำหนด: หรือ

นอกเหนือจากคำจำกัดความแล้ว หากเวกเตอร์เป็นแบบแนวเส้นตรง เมื่อพิจารณารูปสี่เหลี่ยมด้านขนาน (แบบมีเงื่อนไข) ก็เป็นเรื่องปกติที่จะกำหนดพื้นที่เป็นศูนย์ ดังนั้น ผลคูณเวกเตอร์ของเวกเตอร์คอลลิเนียร์จึงถือว่าเท่ากับเวกเตอร์ว่าง

เนื่องจากเวกเตอร์ว่างสามารถกำหนดทิศทางใดก็ได้ ข้อตกลงนี้จึงไม่ขัดแย้งกับคำจำกัดความของย่อหน้าที่ 2 และ 3

หมายเหตุ 1. ในคำว่า “ผลิตภัณฑ์ข้าม” คำแรกบ่งชี้ว่าผลลัพธ์ของการกระทำนั้นเป็นเวกเตอร์ (ซึ่งตรงข้ามกับ ผลิตภัณฑ์สเกลาร์- พ § 104 หมายเหตุ 1)

ตัวอย่างที่ 1 ค้นหาผลคูณเวกเตอร์โดยที่เวกเตอร์หลักของระบบพิกัดที่ถูกต้อง (รูปที่ 156)

1. เนื่องจากความยาวของเวกเตอร์หลักเท่ากับหนึ่งหน่วยมาตราส่วน พื้นที่ของสี่เหลี่ยมด้านขนาน (สี่เหลี่ยมจัตุรัส) จึงเป็นตัวเลขเท่ากับหนึ่ง ซึ่งหมายความว่าโมดูลัสของผลิตภัณฑ์เวกเตอร์มีค่าเท่ากับหนึ่ง

2. เนื่องจากตั้งฉากกับระนาบคือแกน ผลคูณเวกเตอร์ที่ต้องการจึงเป็นเวกเตอร์โคลิเนียร์กับเวกเตอร์ k และเนื่องจากทั้งคู่มีโมดูลัส 1 ผลคูณเวกเตอร์ที่ต้องการจึงเท่ากับ k หรือ -k

3. จากเวกเตอร์ที่เป็นไปได้ทั้งสองนี้ ต้องเลือกเวกเตอร์แรก เนื่องจากเวกเตอร์ k เป็นระบบที่ถนัดขวา (และเวกเตอร์เป็นระบบที่ถนัดซ้าย)

ตัวอย่างที่ 2 ค้นหาผลคูณไขว้

สารละลาย. ดังตัวอย่างที่ 1 เราสรุปได้ว่าเวกเตอร์มีค่าเท่ากับ k หรือ -k แต่ตอนนี้เราต้องเลือก -k เนื่องจากเวกเตอร์สร้างระบบทางขวา (และเวกเตอร์ก่อตัวเป็นระบบทางซ้าย) ดังนั้น,

ตัวอย่างที่ 3 เวกเตอร์มีความยาวเท่ากับ 80 และ 50 ซม. ตามลำดับ และมีมุม 30° นำเมตรเป็นหน่วยของความยาว หาความยาวของผลคูณเวกเตอร์ a

สารละลาย. พื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างบนเวกเตอร์เท่ากับ ความยาวของผลิตภัณฑ์เวกเตอร์ที่ต้องการเท่ากับ

ตัวอย่างที่ 4 ค้นหาความยาวของผลคูณเวกเตอร์ของเวกเตอร์เดียวกัน โดยใช้หน่วยเซนติเมตรเป็นหน่วยความยาว

สารละลาย. เนื่องจากพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างบนเวกเตอร์เท่ากัน ความยาวของผลิตภัณฑ์เวกเตอร์จึงเท่ากับ 2,000 ซม. เช่น

จากการเปรียบเทียบตัวอย่างที่ 3 และ 4 เห็นได้ชัดว่าความยาวของเวกเตอร์ไม่เพียงแต่ขึ้นอยู่กับความยาวของตัวประกอบเท่านั้น แต่ยังขึ้นอยู่กับการเลือกหน่วยความยาวด้วย

ความหมายทางกายภาพของผลิตภัณฑ์เวกเตอร์จากปริมาณทางกายภาพจำนวนมากที่แสดงโดยผลคูณเวกเตอร์ เราจะพิจารณาเฉพาะช่วงเวลาแห่งแรงเท่านั้น

ให้ A เป็นจุดที่ใช้แรง โมเมนต์ของแรงสัมพันธ์กับจุด O เรียกว่าผลคูณเวกเตอร์ เนื่องจากโมดูลัสของผลิตภัณฑ์เวกเตอร์นี้มีตัวเลขเท่ากับพื้นที่ของสี่เหลี่ยมด้านขนาน (รูปที่ 157) โมดูลัสของโมเมนต์เท่ากับผลคูณของฐานและความสูง กล่าวคือ แรงคูณด้วยระยะห่างจากจุด O ถึงเส้นตรงที่แรงกระทำ

ในกลศาสตร์ ได้รับการพิสูจน์แล้วว่าเพื่อความสมดุลของวัตถุแข็งเกร็ง ไม่เพียงแต่ผลรวมของเวกเตอร์ที่เป็นตัวแทนของแรงที่กระทำต่อร่างกายจะต้องเท่ากับศูนย์ แต่ยังรวมถึงผลรวมของโมเมนต์ของแรงด้วย ในกรณีที่แรงทั้งหมดขนานกับระนาบเดียว การบวกเวกเตอร์ที่แทนโมเมนต์สามารถแทนที่ได้ด้วยการบวกและการลบขนาดของพวกมัน แต่ด้วยทิศทางของกองกำลังตามอำเภอใจ การทดแทนดังกล่าวจึงเป็นไปไม่ได้ ด้วยเหตุนี้ ผลคูณเวกเตอร์จึงถูกกำหนดให้เป็นเวกเตอร์อย่างแม่นยำ ไม่ใช่ตัวเลข

ก่อนที่จะให้แนวคิดเกี่ยวกับผลคูณเวกเตอร์ ให้เราหันมาที่คำถามเกี่ยวกับการวางแนวของเวกเตอร์ลำดับสามของ a →, b →, c → ในปริภูมิสามมิติ

ขั้นแรก ให้แยกเวกเตอร์ a → , b → , c → ออกจากจุดหนึ่ง การวางแนวของสาม a → , b → , c → สามารถไปทางขวาหรือซ้ายก็ได้ ขึ้นอยู่กับทิศทางของเวกเตอร์ c → นั่นเอง ประเภทของทริปเปิ้ล a → , b → , c → จะถูกกำหนดจากทิศทางที่เวกเตอร์ a → ถึง b → จากจุดสิ้นสุดของเวกเตอร์ c → หมุนที่สั้นที่สุด

หากหมุนทวนเข็มนาฬิกาสั้นที่สุด ก็จะเรียกเวกเตอร์ทั้งสาม a → , b → , c → ขวาถ้าตามเข็มนาฬิกา – ซ้าย.

จากนั้น หาเวกเตอร์ที่ไม่ใช่คอลลิเนียร์สองตัว a → และ b → จากนั้นให้เราพลอตเวกเตอร์ A B → = a → และ AC → = b → จากจุด A เรามาสร้างเวกเตอร์ A D → = c → ซึ่งตั้งฉากกับทั้ง A B → และ A C → พร้อมกัน ดังนั้น เมื่อสร้างเวกเตอร์ด้วยตัว A D → = c → เราสามารถทำได้สองวิธี โดยกำหนดให้เป็นทิศทางเดียวหรือตรงกันข้าม (ดูภาพประกอบ)

ตามที่เราพบ เวกเตอร์สามเท่าของลำดับ a → , b → , c → สามารถเป็นได้ทั้งทางขวาหรือทางซ้าย ขึ้นอยู่กับทิศทางของเวกเตอร์

จากที่กล่าวมาข้างต้น เราสามารถแนะนำคำจำกัดความของผลิตภัณฑ์เวกเตอร์ได้ คำจำกัดความนี้กำหนดไว้สำหรับเวกเตอร์สองตัวที่กำหนดในระบบพิกัดสี่เหลี่ยมในปริภูมิสามมิติ

คำจำกัดความ 1

ผลคูณเวกเตอร์ของเวกเตอร์สองตัว a → และ b → เราจะเรียกเวกเตอร์ดังกล่าวซึ่งกำหนดไว้ในระบบพิกัดสี่เหลี่ยมของปริภูมิสามมิติดังนี้:

• ถ้าเวกเตอร์ a → และ b → เป็นเส้นตรง มันจะเป็นศูนย์
• มันจะตั้งฉากกับทั้งเวกเตอร์ a → ​​​​ และเวกเตอร์ b → เช่น ∠ ก → ค → = ∠ ข → ค → = π 2 ;
• ความยาวถูกกำหนดโดยสูตร: c → = a → · b → · sin ∠ a → , b → ;
• เวกเตอร์สามเท่า a → , b → , c → มีทิศทางเดียวกับระบบพิกัดที่กำหนด

ผลคูณเวกเตอร์ของเวกเตอร์ a → และ b → มีเครื่องหมายดังนี้: a → × b →

พิกัดของผลิตภัณฑ์เวกเตอร์

เนื่องจากเวกเตอร์ใดๆ มีพิกัดที่แน่นอนในระบบพิกัด เราจึงสามารถแนะนำคำจำกัดความที่สองของผลิตภัณฑ์เวกเตอร์ได้ ซึ่งจะช่วยให้เราค้นหาพิกัดของมันโดยใช้พิกัดที่กำหนดของเวกเตอร์ได้

คำจำกัดความ 2

ในระบบพิกัดสี่เหลี่ยมของปริภูมิสามมิติ ผลคูณเวกเตอร์ของเวกเตอร์สองตัว a → = (a x ; a y ; a z) และ b → = (b x ; b y ; b z) เรียกว่าเวกเตอร์ c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → โดยที่ i → , j → , k → เป็นเวกเตอร์พิกัด

ผลคูณเวกเตอร์สามารถแสดงเป็นตัวดีเทอร์มิแนนต์ของเมทริกซ์จตุรัสลำดับที่สาม โดยที่แถวแรกประกอบด้วยเวกเตอร์เวกเตอร์ i → , j → , k → แถวที่สองประกอบด้วยพิกัดของเวกเตอร์ a → และแถวที่สาม มีพิกัดของเวกเตอร์ b → ในระบบพิกัดสี่เหลี่ยมที่กำหนด นี่คือดีเทอร์มีแนนต์ของเมทริกซ์มีลักษณะดังนี้: c → = a → × b → = i → j → k → a x a y a z b x b y b z

เมื่อขยายดีเทอร์มิแนนต์นี้เข้าไปในองค์ประกอบของแถวแรก เราจะได้ความเท่าเทียมกัน: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (มี b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

คุณสมบัติของผลิตภัณฑ์ข้าม

เป็นที่ทราบกันดีว่าผลคูณเวกเตอร์ในพิกัดนั้นแสดงเป็นตัวกำหนดของเมทริกซ์ c → = a → × b → = i → j → k → a x a y a z b x b y b z จากนั้นบนพื้นฐาน คุณสมบัติของตัวกำหนดเมทริกซ์ต่อไปนี้จะปรากฏขึ้น คุณสมบัติของผลิตภัณฑ์เวกเตอร์:

1. การต่อต้านการกลายพันธุ์ a → × b → = - b → × a → ;
2. การกระจายตัว a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → หรือ a → × b (1) → + b (2) → = a → × ข (1) → + ก → × ข (2) → ;
3. ความเชื่อมโยง แลมบ์ดา → × b → = แลมบ์ → × b → หรือ a → × (แลม b →) = แลมบ์ → × b → โดยที่ แลมคือจำนวนจริงใดๆ ก็ตาม

คุณสมบัติเหล่านี้มีการพิสูจน์ง่ายๆ

ตามตัวอย่าง เราสามารถพิสูจน์คุณสมบัติต้านการเปลี่ยนแปลงของผลิตภัณฑ์เวกเตอร์ได้

หลักฐานการต่อต้านการเปลี่ยนแปลง

ตามคำนิยาม a → × b → = i → j → k → a x a y a z b x b y b z และ b → × a → = i → j → k → b x b y b z a x a y a z และถ้ามีการสลับเมทริกซ์สองแถว ค่าของดีเทอร์มิแนนต์ของเมทริกซ์ควรเปลี่ยนไปตรงกันข้าม ดังนั้น a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → ซึ่งและพิสูจน์ว่าผลคูณเวกเตอร์เป็นแบบต้านการเปลี่ยนแปลง

ผลิตภัณฑ์เวกเตอร์ - ตัวอย่างและวิธีแก้ปัญหา

ในกรณีส่วนใหญ่ จะมีปัญหาสามประเภท

ในโจทย์ประเภทแรก มักจะให้ความยาวของเวกเตอร์สองตัวและมุมระหว่างเวกเตอร์เหล่านั้น และคุณจำเป็นต้องค้นหาความยาวของผลคูณเวกเตอร์ ในกรณีนี้ ให้ใช้สูตรต่อไปนี้ c → = a → · b → · sin ∠ a → , b →

ตัวอย่างที่ 1

จงหาความยาวของผลคูณเวกเตอร์ของเวกเตอร์ a → และ b → ถ้าคุณรู้ a → = 3, b → = 5, ∠ a →, b → = π 4

สารละลาย

โดยการหาความยาวของผลคูณเวกเตอร์ของเวกเตอร์ a → และ b → เราจะแก้ปัญหานี้: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

คำตอบ: 15 2 2 .

ปัญหาประเภทที่สองมีความเกี่ยวข้องกับพิกัดของเวกเตอร์ โดยในนั้นคือผลคูณเวกเตอร์ ความยาวของมัน ฯลฯ ค้นหาผ่าน พิกัดที่ทราบเวกเตอร์ที่กำหนด ก → = (ก x; ก y; ก z) และ ข → = (ข x ; โดย ; ข z) .

สำหรับปัญหาประเภทนี้ คุณสามารถแก้ไขตัวเลือกงานได้มากมาย ตัวอย่างเช่น ไม่สามารถระบุพิกัดของเวกเตอร์ a → และ b → ได้ แต่จะระบุการขยายในเวกเตอร์นั้น พิกัดเวกเตอร์พิมพ์ b → = b x · i → + b y · j → + b z · k → และ c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → หรือเวกเตอร์ a → และ b → สามารถระบุได้ด้วยพิกัดจุดเริ่มต้น และจุดสิ้นสุด

ลองพิจารณาตัวอย่างต่อไปนี้

ตัวอย่างที่ 2

ในระบบพิกัดสี่เหลี่ยม ให้เวกเตอร์สองตัว: a → = (2; 1; - 3), b → = (0; - 1; 1) ค้นหาผลิตภัณฑ์ข้ามของพวกเขา

สารละลาย

ตามคำจำกัดความที่สอง เราจะพบผลคูณเวกเตอร์ของเวกเตอร์สองตัวในพิกัดที่กำหนด: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · by - ay · bx) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

ถ้าเราเขียนผลคูณเวกเตอร์ในรูปของดีเทอร์มีแนนต์ของเมทริกซ์ แล้วคำตอบ ตัวอย่างนี้มีลักษณะดังนี้: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k →

คำตอบ: ก → × b → = - 2 ผม → - 2 เจ → - 2 k → .

ตัวอย่างที่ 3

จงหาความยาวของผลคูณเวกเตอร์ของเวกเตอร์ i → - j → และ i → + j → + k → โดยที่ i →, j →, k → เป็นเวกเตอร์หน่วยของระบบพิกัดคาร์ทีเซียนสี่เหลี่ยม

สารละลาย

ก่อนอื่น เรามาค้นหาพิกัดของผลิตภัณฑ์เวกเตอร์ที่กำหนด i → - j → × i → + j → + k → ในระบบพิกัดสี่เหลี่ยมที่กำหนด

เป็นที่ทราบกันว่าเวกเตอร์ i → - j → และ i → + j → + k → มีพิกัด (1; - 1; 0) และ (1; 1; 1) ตามลำดับ ลองหาความยาวของผลคูณเวกเตอร์โดยใช้ดีเทอร์มิแนนต์ของเมทริกซ์ จากนั้นเราจะได้ i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - เจ → + 2 k → .

ดังนั้น ผลคูณเวกเตอร์ i → - j → × i → + j → + k → มีพิกัด (- 1 ; - 1 ; 2) ในระบบพิกัดที่กำหนด

เราค้นหาความยาวของผลคูณเวกเตอร์โดยใช้สูตร (ดูหัวข้อการหาความยาวของเวกเตอร์): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

คำตอบ: ผม → - เจ → × ผม → + เจ → + k → = 6 . -

ตัวอย่างที่ 4

ในระบบพิกัดคาร์ทีเซียนสี่เหลี่ยม พิกัดสามจุด A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) จะได้รับ จงหาเวกเตอร์ที่ตั้งฉากกับ A B → และ A C → ในเวลาเดียวกัน

สารละลาย

เวกเตอร์ A B → และ AC → มีพิกัดต่อไปนี้ (- 1 ; 2 ; 2) และ (0 ; 4 ; 1) ตามลำดับ เมื่อพบผลคูณเวกเตอร์ของเวกเตอร์ A B → และ A C → ก็เห็นได้ชัดว่าเป็นเช่นนั้น เวกเตอร์ตั้งฉากตามคำนิยาม ทั้ง A B →​​​​ และ A C → นั่นก็คือเป็นวิธีการแก้ปัญหาของเรา ลองหามันมา A B → × AC → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

คำตอบ: - 6 ผม → + เจ → - 4 k → . - หนึ่งในเวกเตอร์ตั้งฉาก

ปัญหาประเภทที่สามจะเน้นไปที่การใช้คุณสมบัติของผลคูณเวกเตอร์ของเวกเตอร์ หลังจากสมัครแล้วเราจะได้แนวทางแก้ไขปัญหาที่กำหนด

ตัวอย่างที่ 5

เวกเตอร์ a → และ b → ตั้งฉากกัน และมีความยาวเท่ากับ 3 และ 4 ตามลำดับ จงหาความยาวของผลคูณเวกเตอร์ 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · ก → × - 2 · ข → + - ข → × ก → + - ข → × - 2 · ข → .

สารละลาย

ด้วยคุณสมบัติการกระจายของผลิตภัณฑ์เวกเตอร์ เราสามารถเขียนได้ 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 ก → × ก → + 3 ก → × - 2 ข → + - ข → × ก → + - ข → × - 2 ข →

ด้วยคุณสมบัติของการเชื่อมโยงเราจะนำค่าสัมประสิทธิ์ตัวเลขออกจากเครื่องหมายของผลิตภัณฑ์เวกเตอร์ในนิพจน์สุดท้าย: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - ข → × - 2 · ข → = = 3 · ก → × ก → + 3 · (- 2) · ก → × ข → + (- 1) · ข → × ก → + (- 1) · (- 2) · ข → × ข → = = 3 ก → × ก → - 6 ก → × ข → - ข → × ก → + 2 ข → × ข →

ผลคูณเวกเตอร์ a → × a → และ b → × b → เท่ากับ 0 เนื่องจาก a → × a → = a → · a → · sin 0 = 0 และ b → × b → = b → · b → · sin 0 = 0 จากนั้น 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → -

จากการต้านคอมมิวทิวิตี้ของผลิตภัณฑ์เวกเตอร์ดังนี้ - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × ข → . -

เมื่อใช้คุณสมบัติของผลคูณเวกเตอร์ เราจะได้ความเท่าเทียมกัน 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

ตามเงื่อนไข เวกเตอร์ a → และ b → ตั้งฉากกัน นั่นคือมุมระหว่างพวกมันเท่ากับ π 2 ตอนนี้สิ่งที่เหลืออยู่คือการแทนที่ค่าที่พบเป็นสูตรที่เหมาะสม: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · บาป (a → , b →) = 5 · 3 · 4 · บาป π 2 = 60 .

คำตอบ: 3 ก → - ข → × ก → - 2 ข → = 60

ความยาวของผลคูณเวกเตอร์ของเวกเตอร์ตามคำจำกัดความ เท่ากับ a → × b → = a → · b → · sin ∠ a → , b → เนื่องจากเป็นที่ทราบกันดีอยู่แล้ว (จากหลักสูตรของโรงเรียน) ว่าพื้นที่ของรูปสามเหลี่ยมเท่ากับครึ่งหนึ่งของผลคูณของความยาวของทั้งสองด้านคูณด้วยไซน์ของมุมระหว่างด้านเหล่านี้ ดังนั้นความยาวของผลคูณเวกเตอร์จึงเท่ากับพื้นที่ของสี่เหลี่ยมด้านขนาน - สามเหลี่ยมสองเท่าคือผลคูณของด้านข้างในรูปแบบของเวกเตอร์ a → และ b → วางลงจากจุดหนึ่งโดยไซน์ของ มุมระหว่างพวกเขา บาป ∠ a →, b →

นี่คือความหมายทางเรขาคณิตของผลิตภัณฑ์เวกเตอร์

ความหมายทางกายภาพของผลิตภัณฑ์เวกเตอร์

ในกลศาสตร์ซึ่งเป็นสาขาหนึ่งของฟิสิกส์ ต้องขอบคุณผลคูณเวกเตอร์ คุณสามารถกำหนดโมเมนต์ของแรงสัมพันธ์กับจุดในอวกาศได้

คำจำกัดความ 3

เมื่อถึงโมเมนต์ของแรง F → ที่ใช้กับจุด B สัมพันธ์กับจุด A เราจะเข้าใจผลคูณเวกเตอร์ต่อไปนี้ A B → × F →

หากคุณสังเกตเห็นข้อผิดพลาดในข้อความ โปรดไฮไลต์แล้วกด Ctrl+Enter

ภาษาอังกฤษ: Wikipedia กำลังทำให้ไซต์มีความปลอดภัยมากขึ้น คุณกำลังใช้เว็บเบราว์เซอร์รุ่นเก่าซึ่งจะไม่สามารถเชื่อมต่อกับวิกิพีเดียได้ในอนาคต โปรดอัปเดตอุปกรณ์ของคุณหรือติดต่อผู้ดูแลระบบไอทีของคุณ

中文: 以下提供更长，更具技术性的更新（仅英语）。

สเปน: Wikipedia está haciendo el sitio más seguro. Usted está utilizando un navegador web viejo que no será capaz de conectarse a Wikipedia en el futuro. Actualice su dispositivo o contacte a su administrador informático. Más abajo hay unaactualización más larga y más técnica en inglés.

ﺎﻠﻋﺮﺒﻳﺓ: ويكيبيديا تسعى لتأمين الموقع أكثر من ذي قبل. أنت تستخدم متصفح وب قديم لن يتمكن من الاتصال بموقع ويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بغداري تقنية المعلومات الخاص بك. يوجد تحديث فني أطول ومغرق في التقنية باللغة الإنجليزية تاليا.

ฝรั่งเศส: Wikipédia va bientôt augmenter la securité de son site. Vous utilisez actuellement un exploreur web ancien, qui ne pourra plus se เชื่อมต่อ à Wikipédia lorsque ce sera fait. Merci de mettre à jour votre appareil ou de contacter votre administrateur informatique à cette fin. ข้อมูลเสริมพร้อมทั้งเทคนิคและภาษาอังกฤษอื่นๆ

日本語: ??????????????????????????????????????????????????????????????????????????????????????

เยอรมัน: Wikipedia erhöht die Sicherheit der เว็บไซต์ Du benutzt einen alten Webbrowser, der in Zukunft nicht mehr auf Wikipedia zugreifen können wird. Bitte Aktualisiere เป็นผู้รับผิดชอบด้าน IT-Administrator และ Ausführlichere (และ technisch detailliertere) Hinweise พบ Du unten ในภาษาอังกฤษ Sprache

อิตาเลียโน่:วิกิพีเดีย sta rendendo il sito più sicuro ใช้เบราว์เซอร์เว็บ che non sarà ใน grado di connettersi และ Wikipedia ในอนาคต ตามที่โปรดปราน aggiorna il tuo dispositivo o contatta il tuo amministratore informatico Più ในบาสโซ è disponibile un aggiornamento più dettagliato e tecnico ในภาษาอิงเกิล

แมกยาร์: Biztonságosabb lesz ในวิกิพีเดีย A böngésző, amit használsz, nem lesz képes kapcsolódni a jövőben. Használj modernebb szoftvert vagy jelezd a problémát a rendszergazdádnak. Alább olvashatod a részletesebb magyarázatot (อันโกลุล).

สเวนสกา:วิกิพีเดีย gör sidan mer säker. Du använder en äldre webbläsare som inte kommer att kunna läsa Wikipedia และ framtiden. อัปเดตข้อมูลติดต่อโดยผู้ดูแลระบบไอที ฟินน์ en längre och mer teknisk förklaring på engelska längre ned.

हिन्दी: विकिपीडिया साइट को और अधिक सुरक्षित बना रहा है। आप एक पुराने वेब ब्राउज़र का उपयोग कर रहे हैं जो भविष्य में विकिपीडिया से कनेक्ट नहीं हो पाएगा। कृपया अपना डिवाइस अपडेट करें या अपने आईटी व्यवस्थापक से संपर्क करें। नीचे अंग्रेजी में एक लंबा और अधिक तकनीकी अद्यतन है।

เรากำลังลบการสนับสนุนสำหรับเวอร์ชันโปรโตคอล TLS ที่ไม่ปลอดภัย โดยเฉพาะ TLSv1.0 และ TLSv1.1 ซึ่งซอฟต์แวร์เบราว์เซอร์ของคุณใช้เชื่อมต่อกับไซต์ของเรา ซึ่งมักเกิดจากเบราว์เซอร์ที่ล้าสมัยหรือสมาร์ทโฟน Android รุ่นเก่า หรืออาจเป็นสัญญาณรบกวนจากซอฟต์แวร์ "ความปลอดภัยทางเว็บ" ขององค์กรหรือส่วนบุคคล ซึ่งจะทำให้ความปลอดภัยในการเชื่อมต่อลดลง

คุณต้องอัปเกรดเว็บเบราว์เซอร์ของคุณหรือแก้ไขปัญหานี้เพื่อเข้าถึงเว็บไซต์ของเรา ข้อความนี้จะคงอยู่จนถึงวันที่ 1 มกราคม 2020 หลังจากวันดังกล่าว เบราว์เซอร์ของคุณจะไม่สามารถสร้างการเชื่อมต่อกับเซิร์ฟเวอร์ของเราได้