Ինչպես հասկանալ, որ ինտեգրալը տարբերվում է: Որոշակի ինտեգրալ առցանց

Առաջին տեսակի ոչ պատշաճ ինտեգրալներ.Որոշակի ինտեգրալի հասկացության ընդլայնում ինտեգրալների դեպքերի վրա, որոնց ինտեգրման անվերջ վերին կամ ստորին սահմանները, կամ ինտեգրման երկու սահմաններն էլ անսահման են:

Երկրորդ տեսակի ոչ պատշաճ ինտեգրալներ.Որոշակի ինտեգրալ հասկացության ընդլայնում անսահմանափակ ֆունկցիաների ինտեգրալների դեպքերի վրա ինտեգրալը գոյություն չունի ինտեգրման վերջավոր հատվածի կետերում, վերածվելով անվերջության.

Համեմատության համար.Որոշակի ինտեգրալի հասկացությունը ներմուծելիս ենթադրվում էր, որ ֆունկցիան զ(x) շարունակական է [ ա, բ], իսկ ինտեգրման հատվածը վերջավոր է, այսինքն՝ սահմանափակված է թվերով, այլ ոչ թե անսահմանությամբ։ Որոշ առաջադրանքներ հանգեցնում են այդ սահմանափակումներից հրաժարվելու անհրաժեշտությանը: Այսպես են հայտնվում ոչ պատշաճ ինտեգրալները։

Անպատշաճ ինտեգրալի երկրաչափական նշանակությունըՊարզվում է բավականին պարզ. Այն դեպքում, երբ ֆունկցիայի գրաֆիկը y = զ(x) առանցքից վեր է Եզ, որոշակի ինտեգրալն արտահայտում է տարածքը կոր trapezoid, սահմանափակված կորով y = զ(x) , x առանցք և օրդինատներ x = ա , x = բ. Իր հերթին, ոչ պատշաճ ինտեգրալն արտահայտում է գծերի միջև պարփակված անսահմանափակ (անսահման) կորագիծ տրապեզիի տարածքը y = զ(x) (ստորև նկարում - կարմիր), x = աև աբսցիսայի առանցքը:

Անպատշաճ ինտեգրալները սահմանվում են նույն կերպ այլ անսահման միջակայքերի համար.

Անսահման կոր trapezoid-ի մակերեսը կարող է լինել վերջավոր թիվ, որի դեպքում ոչ պատշաճ ինտեգրալը կոչվում է կոնվերգենտ: Տարածքը կարող է լինել նաև անվերջություն, և այս դեպքում ոչ պատշաճ ինտեգրալը կոչվում է դիվերգենտ։

Ինտեգրալի սահմանի օգտագործումը ոչ պատշաճ ինտեգրալի փոխարեն:Անպատշաճ ինտեգրալը գնահատելու համար անհրաժեշտ է օգտագործել որոշակի ինտեգրալի սահմանը։ Եթե ​​այս սահմանը գոյություն ունի և վերջավոր է (հավասար չէ անվերջությանը), ապա ոչ պատշաճ ինտեգրալը կոչվում է կոնվերգենտ, իսկ հակառակ դեպքում՝ դիվերգենտ։ Թե ինչի է ձգտում փոփոխականը սահմանային նշանի տակ, կախված է նրանից, թե մենք գործ ունենք առաջին տեսակի ոչ պատշաճ ինտեգրալի հետ, թե երկրորդ տեսակի: Եկեք պարզենք այս մասին հիմա:

Առաջին տեսակի ոչ պատշաճ ինտեգրալներ՝ անսահման սահմաններով և դրանց կոնվերգենցիայով

Սխալ ինտեգրալներ՝ անսահման վերին սահմանով

Այսպիսով, ոչ պատշաճ ինտեգրալ գրելը տարբերվում է սովորական որոշակի ինտեգրալից նրանով, որ ինտեգրման վերին սահմանն անսահման է։

Սահմանում. Ոչ պատշաճ ինտեգրալ՝ շարունակական ֆունկցիայի ինտեգրման անսահման վերին սահմանով զ(x) սկսած միջակայքում ա նախքան ∞ կոչվում է այս ֆունկցիայի ինտեգրալի սահմանը ինտեգրման վերին սահմանի հետ բ և ինտեգրման ստորին սահմանը ա պայմանով, որ ինտեգրման վերին սահմանը աճում է անսահմանափակ, այսինքն.

.

Եթե ​​այս սահմանը գոյություն ունի և հավասար է ինչ-որ թվի, այլ ոչ թե անսահմանության, ապա ոչ պատշաճ ինտեգրալը կոչվում է կոնվերգենտ, և որպես արժեք ընդունվում է այն թիվը, որին հավասար է սահմանը։ Հակառակ դեպքում ոչ պատշաճ ինտեգրալը կոչվում է դիվերգենտև դրան ոչ մի նշանակություն չի վերագրվում։

Օրինակ 1. Հաշվարկել ոչ պատշաճ ինտեգրալը(եթե այն համընկնում է):

Լուծում. Ելնելով ոչ պատշաճ ինտեգրալի սահմանումից՝ մենք գտնում ենք

Քանի որ սահմանը գոյություն ունի և հավասար է 1-ի, ուրեմն սա ոչ պատշաճ ինտեգրալը համընկնում էև հավասար է 1-ի։

IN հետևյալ օրինակըինտեգրանդը գրեթե նույնն է, ինչ օրինակ 1-ում, միայն x աստիճանը երկու չէ, այլ ալֆա տառը, և խնդիրն է ուսումնասիրել ոչ պատշաճ ինտեգրալը կոնվերգենցիայի համար: Այսինքն՝ մնում է պատասխանել հարցին՝ ալֆայի ո՞ր արժեքներով է համընկնում այս ոչ պատշաճ ինտեգրալը, և ի՞նչ արժեքներով է այն շեղվում։

Օրինակ 2. Քննեք անհամապատասխան ինտեգրալը կոնվերգենցիայի համար(ինտեգրման ստորին սահմանը զրոյից մեծ է):

Լուծում. Նախ ենթադրենք, որ այնուհետև

Ստացված արտահայտության մեջ մենք շարժվում ենք դեպի սահմանը՝

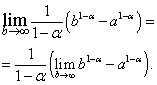
Հեշտ է տեսնել, որ աջ կողմի սահմանը գոյություն ունի և հավասար է զրոյի, երբ, այսինքն, և գոյություն չունի, երբ, այսինքն.

Առաջին դեպքում, այսինքն, երբ . Եթե, ապա և գոյություն չունի:

Մեր ուսումնասիրության եզրակացությունը հետևյալն է ոչ պատշաճ ինտեգրալը համընկնում էժամը և տարբերվում էժամը .

Նյուտոն-Լայբնից բանաձևի կիրառում ուսումնասիրվող ոչ պատշաճ ինտեգրալի տեսակի վրա , կարող եք դուրս բերել հետևյալ բանաձևը, որը շատ նման է դրան.

.

Սա Նյուտոն-Լայբնից ընդհանրացված բանաձև է։

Օրինակ 3. Հաշվարկել ոչ պատշաճ ինտեգրալը(եթե այն համընկնում է):

Այս ինտեգրալի սահմանը գոյություն ունի.

Երկրորդ ինտեգրալը՝ կազմելով սկզբնական ինտեգրալն արտահայտող գումարը.

Այս ինտեգրալի սահմանը նույնպես գոյություն ունի.

.

Մենք գտնում ենք երկու ինտեգրալների գումարը, որը նաև սկզբնական ոչ պատշաճ ինտեգրալի արժեքն է երկու անսահման սահմաններով.

Երկրորդ տեսակի ոչ պատշաճ ինտեգրալներ՝ անսահմանափակ ֆունկցիաներից և դրանց կոնվերգենցիայից

Թողեք գործառույթը զ(x) տրված հատվածի վրա ա նախքան բ և դրա վրա անսահմանափակ է: Ենթադրենք, որ ֆունկցիան կետում գնում է դեպի անսահմանություն բ , մինչդեռ հատվածի մյուս բոլոր կետերում այն ​​շարունակական է։

Սահմանում. Ֆունկցիայի ոչ պատշաճ ինտեգրալ զ(x) -ից հատվածի վրա ա նախքան բ կոչվում է այս ֆունկցիայի ինտեգրալի սահմանը ինտեգրման վերին սահմանի հետ գ , եթե ձգտելիս գ Դեպի բ ֆունկցիան մեծանում է առանց սահմանի, և կետում x = բ գործառույթը սահմանված չէ, այսինքն.

.

Եթե ​​այս սահմանը գոյություն ունի, ապա երկրորդ տեսակի ոչ պատշաճ ինտեգրալը կոչվում է կոնվերգենտ, հակառակ դեպքում՝ դիվերգենտ։

Օգտագործելով Նյուտոն-Լայբնից բանաձևը, մենք բխում ենք.

Որոշակի ինտեգրալ

\[I=\int_a^bf(x)dx \]

կառուցվել է այն ենթադրությամբ, որ $a,\,b$ թվերը վերջավոր են, իսկ $f(x)$-ը շարունակական ֆունկցիա է: Եթե ​​այս ենթադրություններից մեկը խախտվում է, մենք խոսում ենք ոչ պատշաճ ինտեգրալների մասին։

10.1 1-ին տեսակի ոչ պատշաճ ինտեգրալներ

1-ին տեսակի ոչ պատշաճ ինտեգրալ է առաջանում, երբ $a,\,b$ թվերից առնվազն մեկը անվերջ է:

10.1.1 Սահմանում և հիմնական հատկություններ

Եկեք նախ դիտարկենք այն իրավիճակը, երբ ինտեգրման ստորին սահմանը վերջավոր է, իսկ վերին սահմանը հավասար է $+\infty$-ի, մենք մի փոքր ուշ կքննարկենք այլ տարբերակներ: $f(x)$-ի համար, շարունակական բոլոր $x$-ի համար, որոնք մեզ հետաքրքրում են, հաշվի առեք ինտեգրալը

\սկիզբ(հավասարում) I=\int _a^(+\infty)f(x)dx. \quad(19) \label(inf1) \end(հավասարում)

Նախևառաջ պետք է հաստատել այս արտահայտության իմաստը։ Դա անելու համար մենք ներկայացնում ենք գործառույթը

\[ I(N)=\int _a^(N)f(x)dx \]

և հաշվի առեք դրա վարքը $N\rightarrow +\infty$-ի համար:

Սահմանում.

Թող լինի վերջավոր սահման

\[ A=\lim_(N \rightarrow +\infty)I(N)=\lim_(N \rightarrow +\infty)\int _a^(N)f(x)dx. \]

Այնուհետև մենք ասում ենք, որ 1-ին տեսակի անպատշաճ ինտեգրալը (19) կոնվերգենտ է և նրան հատկացվում է $A$ արժեքը, որն ինքնին կոչվում է ինտեգրելի $\left[a, \, +\infty \right) միջակայքում. $. Եթե ​​նշված սահմանաչափը գոյություն չունի կամ այն ​​հավասար է $\pm \infty$-ի, ապա ասում են, որ ինտեգրալը (19) շեղվում է:

Դիտարկենք ինտեգրալը

\[ I=\int _0^(+\infty) \frac(dx)(1+x^2): \]

IN \[ I(N)=\int _0^(N) \frac(dx)(1+x^2): \]այս դեպքում

ինտեգրանդ ֆունկցիայի հակաածանցյալը հայտնի է, ուստի

\[ I(N)=\int _0^(N) \frac(dx)(1+x^2)=arctgx|_0^(N)=arctgN. \]

Հայտնի է, որ $arctg N \rightarrow \pi /2 $ $N \rightarrow +\infty$-ի դիմաց։ Այսպիսով, $I(N)$-ն ունի վերջավոր սահման, մեր ոչ պատշաճ ինտեգրալը համընկնում է և հավասար է $\pi /2$-ի:

1. Եթե $f(x)$, $g(x)$-ը ինտեգրելի են $\left[ a, \, +\infty \right)$ միջակայքում, ապա դրանց գումարը $f(x)+g(x) $-ը նույնպես ինտեգրելի է այս միջակայքում, և \[ \int _a^(+\infty)\left(f(x)+g(x)\right)dx=\int _a^(+\infty)f(x )dx+\int _a^(+\infty)g(x)dx. \] 2. Եթե $f(x)$-ը ինտեգրելի է $\left[a, \, +\infty \right)$ միջակայքում, ապա ցանկացած հաստատուն $C$-ի համար $C\cdot f(x)$ ֆունկցիան նույնպես ինտեգրելի է այս միջակայքում, և \[ \int _a^(+\infty)C\cdot f(x)dx=C \cdot \int _a^(+\infty)f(x)dx: \] 3. Եթե $f(x)$-ը ինտեգրելի է $\left[a, \, +\infty \right)$ միջակայքում, և այս միջակայքում $f(x)>0$, ապա \[ \int _a^ (+\infty) f(x)dx\,>\,0. \] 4. Եթե $f(x)$-ը ինտեգրելի է $\left[ a, \, +\infty \right)$ միջակայքում, ապա ցանկացած $b>a$-ի համար ինտեգրալը \[ \int _b^(+ \infty) f(x)dx \] համընկնում է, և \[ \int _a^(+\infty)f(x)dx=\int _a^(b) f(x)dx+\int _b^(+\infty) ) f( x)dx \] (ինտեգրալի հավելում միջակայքում):

Գործում են նաև փոփոխականի փոփոխության, մասերի ինտեգրման և այլնի բանաձևերը։ (բնական վերապահումներով):

Այնուհետև մենք ասում ենք, որ 1-ին տեսակի անպատշաճ ինտեգրալը (19) կոնվերգենտ է և նրան հատկացվում է $A$ արժեքը, որն ինքնին կոչվում է ինտեգրելի $\left[a, \, +\infty \right) միջակայքում. $. Եթե ​​նշված սահմանաչափը գոյություն չունի կամ այն ​​հավասար է $\pm \infty$-ի, ապա ասում են, որ ինտեգրալը (19) շեղվում է:

\սկիզբ(հավասարում) I=\int _1^(+\infty)\frac(1)(x^k)\,dx. \quad (20) \label(mod) \վերջ (հավասարում)

Ներկայացնենք ֆունկցիան

\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx. \]

Այս դեպքում հայտնի է հակաածանցյալը, ուրեմն

\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k)|_1^N = \frac(N^(1-k))(1-k)-\frac(1)(1-k) \]

$k \neq 1$-ի դիմաց,

\[ I(N)=\int _1^(N)\frac(1)(x)\,dx\,=lnx|_1^N= lnN \]

$k = 1$-ի համար: Հաշվի առնելով $N \rightarrow +\infty$-ի վարքագիծը, մենք գալիս ենք այն եզրակացության, որ ինտեգրալը (20) համընկնում է $k>1$-ի համար և շեղվում է $k \leq 1$-ի համար:

Այժմ դիտարկենք այն տարբերակը, երբ ինտեգրման ստորին սահմանը հավասար է $-\infty$-ի, իսկ վերինը՝ վերջավոր, այսինքն. եկեք դիտարկենք ինտեգրալները

\[ I=\int _(-\infty)^af(x)dx. \]

Այնուամենայնիվ, այս տարբերակը կարող է կրճատվել նախորդի վրա, եթե մենք փոխենք $x=-s$ փոփոխականները և այնուհետև փոխենք ինտեգրման սահմանները տեղերում, այնպես որ.

\[ I=\int _(-a)^(+\infty)g(s)ds, \]

$g(s)=f(-s)$. Այժմ դիտարկենք այն դեպքը, երբ կան երկու անսահման սահմաններ, այսինքն. անբաժանելի

\սկիզբ(հավասարում) I=\int _(-\infty)^(+\infty)f(x)dx, \quad (21) \label(intr) \end(հավասարում)

իսկ $f(x)$-ը շարունակական է բոլոր $x \in \mathbb(R)$-ի համար: Եկեք բաժանենք միջակայքը երկու մասի. վերցնենք $c \in \mathbb(R)$ և դիտարկենք երկու ինտեգրալ,

\[ I_1=\int _(-\infty)^(c)f(x)dx, \quad I_2=\int _(c)^(+\infty)f(x)dx. \]

Սահմանում.

Եթե ​​$I_1$, $I_2$ երկու ինտեգրալները համընկնում են, ապա ինտեգրալը (21) կոչվում է կոնվերգենտ և նրան վերագրվում է $I=I_1+I_2$ արժեքը (համաձայն միջակայքի հավելումների)։ Եթե ​​$I_1$, $I_2$ ինտեգրալներից գոնե մեկը շեղվում է, ապա ինտեգրալը (21) կոչվում է դիվերգենտ:

Կարելի է ապացուցել, որ ինտեգրալի (21) կոնվերգենցիան կախված չէ $c$ կետի ընտրությունից։

1-ին տեսակի ոչ պատշաճ ինտեգրալները $\left(-\infty, \, c \right]$ կամ $(-\infty, \, +\infty)$ ինտեգրման միջակայքերով ունեն նաև որոշակի ինտեգրալների բոլոր ստանդարտ հատկությունները (հետ համապատասխան վերակազմակերպում՝ հաշվի առնելով ընտրության ինտեգրման միջակայքը):

10.1.2 1-ին տեսակի ոչ պատշաճ ինտեգրալների կոնվերգենցիայի թեստեր

Թեորեմ (համեմատության առաջին նշանը). Թող $f(x)$, $g(x)$ շարունակական լինեն $x>a$-ի և $0 a$-ի համար: Հետո

1. Եթե \[ \int _a^(+\infty)g(x)dx \] ինտեգրալը համընկնում է, ապա \[ \int _a^(+\infty)f(x)dx ինտեգրալը համընկնում է։ \] 2. Եթե \[ \int _a^(+\infty)f(x)dx \] ինտեգրալը շեղվում է, ապա \[ \int _a^(+\infty)g(x)dx ինտեգրալը շեղվում է։ \]

Թեորեմ (համեմատության երկրորդ չափանիշ): Թող $f(x)$, $g(x)$ լինի շարունակական և դրական $x>a$-ի համար, և թող լինի վերջավոր սահման

\[ \theta = \lim_(x \rightarrow +\infty) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Հետո ինտեգրալները

\[ \int _a^(+\infty)f(x)dx, \quad \int _a^(+\infty)g(x)dx \]

Այնուհետև մենք ասում ենք, որ 1-ին տեսակի անպատշաճ ինտեգրալը (19) կոնվերգենտ է և նրան հատկացվում է $A$ արժեքը, որն ինքնին կոչվում է ինտեգրելի $\left[a, \, +\infty \right) միջակայքում. $. Եթե ​​նշված սահմանաչափը գոյություն չունի կամ այն ​​հավասար է $\pm \infty$-ի, ապա ասում են, որ ինտեգրալը (19) շեղվում է:

համընկնել կամ շեղվել միաժամանակ.

\[ I=\int _1^(+\infty)\frac(1)(x+\sin x)\,dx. \]

Ինտեգրանդը դրական ֆունկցիա է ինտեգրման միջակայքի վրա: Ավելին, $x \rightarrow +\infty$-ի համար մենք ունենք.

$\sin x$-ը հայտարարի «փոքր» ուղղում է: Ավելի ճիշտ, եթե վերցնենք $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$, ապա

\[ \lim _(x \rightarrow +\infty)\frac(f(x))(g(x))=\lim _(x \rightarrow +\infty)\frac(x)(x+\sin x) =1. \]

Կիրառելով համեմատության երկրորդ չափանիշը՝ մենք գալիս ենք այն եզրակացության, որ մեր ինտեգրալը զուգակցվում կամ շեղվում է ինտեգրալի հետ միաժամանակ.

\[ \int _1^(+\infty)\frac(1)(x)\,dx . \]

Ինչպես ցույց տրվեց նախորդ օրինակում, այս ինտեգրալը տարբերվում է ($k=1$): Հետևաբար, սկզբնական ինտեգրալը տարբերվում է։

1. \[ \int _(0)^(+\infty)e^(-ax)\,dx. \] 2. \[ \int _(0)^(+\infty)xe^(-x^2)\,dx. \] 3. \[ \int _(-\infty)^(+\infty)\frac(2xdx)(x^2+1): \] 4. \[ \int _(0)^(+\infty)\frac(xdx)((x+2)^3): \] 5. \[ \int _(-\infty)^(+\infty)\frac(dx)(x^2+2x+2): \] 6. \[ \int _(1)^(+\infty)\frac(lnx)(x^2)\,dx. \] 7. \[ \int _(1)^(+\infty)\frac(dx)((1+x)\sqrt(x)): \] 8. \[ \int _(0)^(+\infty)e^(-\sqrt(x))\,dx. \] 9. \[ \int _(0)^(+\infty)e^(-ax)\cos x\,dx. \] 10. \[ \int _(0)^(+\infty)\frac(xdx)(x^3+1): \]

Դուք հիմա այստեղ եք: =) Ոչ, ես չէի փորձում որևէ մեկին վախեցնել, պարզապես ոչ պատշաճ ինտեգրալների թեման շատ է գեղեցիկ նկարազարդումորքան կարևոր է չանտեսել բարձրագույն մաթեմատիկան և այլ ճշգրիտ գիտությունները: Այն ամենը, ինչ ձեզ անհրաժեշտ է դասը սովորելու համար, կայքում է՝ մանրամասն և մատչելի ձևով, եթե ցանկանում եք...

Այսպիսով, եկեք սկսենք. Պատկերավոր ասած՝ ոչ պատշաճ ինտեգրալը «առաջադեմ» որոշակի ինտեգրալ է, և իրականում դրանց հետ կապված դժվարություններն այնքան էլ շատ չեն, և բացի այդ, ոչ պատշաճ ինտեգրալը շատ լավ երկրաչափական նշանակություն ունի։

Ի՞նչ է նշանակում գնահատել ոչ պատշաճ ինտեգրալը:

Հաշվարկել ոչ պատշաճ ինտեգրալը - սա նշանակում է գտնել ԹԻՎԸ(ճիշտ նույնը, ինչ որոշակի ինտեգրալում), կամ ապացուցել, որ այն տարբերվում է(այսինքն՝ թվի փոխարեն հայտնվում ես անսահմանությամբ):

Անպատշաճ ինտեգրալների երկու տեսակ կա.

Անպատշաճ ինտեգրալ՝ ինտեգրման անսահման սահման(ներ)ով

Երբեմն նման ոչ պատշաճ ինտեգրալը կոչվում է առաջին տեսակի ոչ պատշաճ ինտեգրալ. IN ընդհանուր տեսարանԱնսահման սահմանով ոչ պատշաճ ինտեգրալն ամենից հաճախ այսպիսի տեսք ունի. Ինչո՞վ է այն տարբերվում որոշակի ինտեգրալից: Վերին սահմանին. Անվերջ է.

Ավելի քիչ տարածված են անսահման ստորին սահմաններով կամ երկու անսահման սահմաններով ինտեգրալները. և մենք կդիտարկենք դրանք ավելի ուշ, երբ հասկանաք:

Դե, հիմա եկեք նայենք ամենատարածված դեպքին. Օրինակների ճնշող մեծամասնության մեջ ինտեգրանդի ֆունկցիան շարունակականարանքում և այս մեկը կարևոր փաստնախ պետք է ստուգել!Որովհետեւ եթե կան բացեր, ապա լրացուցիչ նրբերանգներ կան։ Որոշակիության համար մենք ենթադրում ենք, որ նույնիսկ այն ժամանակ բնորոշ կոր trapezoidկունենա հետևյալ տեսքը.

Նկատի ունեցեք, որ այն անսահման է (աջից սահմանափակված չէ), և ոչ պատշաճ ինտեգրալթվայինորեն հավասար է իր տարածքին. Հետևյալ տարբերակները հնարավոր են.

1) Առաջին միտքը, որ գալիս է մտքում. «քանի որ գործիչը անսահման է, ուրեմն «Այսինքն՝ տարածքն էլ է անսահման։ Կարող է այդպես լինել։Այս դեպքում ասում են, որ ոչ պատշաճ ինտեգրալը տարբերվում է.

2) Բայց. Որքան էլ պարադոքսալ հնչի, տարածքը անվերջ գործիչկարող է հավասար լինել… վերջավոր թիվ: Օրինակ: ։ Սա կարո՞ղ է ճիշտ լինել: Հեշտությամբ։ Երկրորդ դեպքում՝ ոչ պատշաճ ինտեգրալը համընկնում է.

3) Երրորդ տարբերակի մասին մի փոքր ուշ։

Ո՞ր դեպքերում է անպատշաճ ինտեգրալը տարբերվում և ո՞ր դեպքերում է այն մերձենում: Դա կախված է ինտեգրանդից, և կոնկրետ օրինակներմենք շատ շուտով կանդրադառնանք դրան:

Ի՞նչ է պատահում, եթե առանցքի տակ գտնվող անսահման կոր trapezoid է: Այս դեպքում ոչ պատշաճ ինտեգրալը (շեղվում է) կամ հավասար է վերջավոր բացասական թվի։

Այսպիսով, ոչ պատշաճ ինտեգրալը կարող է բացասական լինել.

Կարևոր.Երբ ձեզ տրվում է ՈՐԵՎԷ ոչ պատշաճ ինտեգրալ լուծելու համար, ապա, ընդհանուր առմամբ, Որևէ տարածքի մասին խոսք չկա և գծանկար կառուցելու կարիք չկա. Ես բացատրեցի ոչ պատշաճ ինտեգրալի երկրաչափական նշանակությունը միայն նյութը հասկանալը հեշտացնելու համար:

Քանի որ ոչ պատշաճ ինտեգրալը շատ նման է որոշակի ինտեգրալին, եկեք հիշենք Նյուտոն-Լայբնից բանաձևը. . Փաստորեն, բանաձևը կիրառելի է նաև ոչ պատշաճ ինտեգրալների համար, միայն թե այն պետք է մի փոքր փոփոխվի։ Որն է տարբերությունը? Ինտեգրման անսահման վերին սահմանում. Հավանաբար, շատերը կռահեցին, որ սա արդեն սահմանների տեսության կիրառման հոտ է գալիս, և բանաձևը կգրվի այսպես. .

Ո՞րն է տարբերությունը որոշակի ինտեգրալից: Առանձնապես ոչինչ! Ինչպես որոշակի ինտեգրալում, դուք պետք է կարողանաք գտնել հակաածանցյալ ֆունկցիան ( անորոշ ինտեգրալ), կարողանալ կիրառել Նյուտոն-Լայբնից բանաձեւը։ Միակ բանը, որ ավելացվել է, սահմանաչափի հաշվարկն է։ Ով նրանց հետ վատ ժամանակ է անցկացնում, դաս քաղի Գործառույթների սահմանները. Լուծումների օրինակներ, որովհետև ավելի լավ է ուշ, քան բանակում.

Դիտարկենք երկու դասական օրինակ.

Օրինակ 1

Պարզության համար գծագրեմ գծանկար, թեև ևս մեկ անգամ շեշտում եմ. պրակտիկայի վրա Այս առաջադրանքում գծագրեր կառուցելու կարիք չկա.

Ինտեգրանդի ֆունկցիան շարունակական է կիսամյակային միջակայքում, ինչը նշանակում է, որ ամեն ինչ լավ է, և սխալ ինտեգրալը կարելի է հաշվարկել «ստանդարտ» մեթոդով։

Մեր բանաձևի կիրառումը և խնդրի լուծումն ունի հետևյալ տեսքը.

Այսինքն, ոչ պատշաճ ինտեգրալը շեղվում է, և ստվերավորված կոր trapezoid-ի մակերեսը հավասար է անսահմանության:

Դիտարկված օրինակում մենք ունենք ամենապարզ աղյուսակի ինտեգրալը և Նյուտոն-Լայբնից բանաձևի կիրառման նույն տեխնիկան, ինչ որոշակի ինտեգրալում: Բայց այս բանաձեւը կկիրառվի սահմանի նշանի տակ։ «Դինամիկ» փոփոխականի սովորական տառի փոխարեն հայտնվում է «be» տառը: Սա չպետք է շփոթեցնի կամ շփոթեցնի, քանի որ ցանկացած տառ ավելի վատ չէ, քան ստանդարտ «X»-ը:

Եթե ​​դուք չեք հասկանում, թե ինչու է , ապա սա շատ վատ է, կամ դուք չեք հասկանում ամենապարզ սահմանները (և ընդհանրապես չեք հասկանում, թե ինչ է սահմանը), կամ չգիտեք, թե ինչ տեսք ունի գրաֆիկը լոգարիթմական ֆունկցիա. Երկրորդ դեպքում՝ հաճախեք դասի Տարրական ֆունկցիաների գրաֆիկները և հատկությունները.

Ոչ պատշաճ ինտեգրալներ լուծելիս շատ կարևոր է իմանալ, թե ինչ տեսք ունեն հիմնական ինտեգրալների գրաֆիկները։ տարրական գործառույթներ!

Ավարտված առաջադրանքը պետք է նման լինի հետևյալին.

“

! Օրինակ պատրաստելիս մենք միշտ ընդհատում ենք լուծումը և նշում, թե ինչ է կատարվում ինտեգրանդի հետ – այն շարունակական է ինտեգրման միջակայքում, թե ոչ։. Սրանով մենք բացահայտում ենք ոչ պատշաճ ինտեգրալի տեսակը և հիմնավորում հետագա գործողությունները։

Օրինակ 2

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Եկեք նկարենք.

Նախ, մենք նշում ենք հետևյալը. ինտեգրանդը շարունակական է կիսամյակային միջակայքում: Գլխարկ. Մենք լուծում ենք բանաձևով :

(1) Մենք վերցնում ենք հզորության ֆունկցիայի ամենապարզ ինտեգրալը (այս հատուկ դեպքը շատ աղյուսակներում է): Ավելի լավ է մինուս նշանը անմիջապես տեղափոխել սահմանային նշանից այն կողմ, որպեսզի հետագա հաշվարկներում այն ​​չխանգարի։

(2) Մենք փոխարինում ենք վերին և ստորին սահմանները՝ օգտագործելով Newton-Leibniz բանաձևը:

(3) Մենք նշում ենք, որ (Պարոնայք, սա վաղուց պետք է հասկանալի լիներ) և պարզեցնում ենք պատասխանը։

Այստեղ անսահման կոր trapezoid-ի մակերեսը վերջավոր թիվ է: Անհավատալի, բայց իրական.

Ավարտված օրինակը պետք է նման լինի հետևյալին.

“

Ինտեգրանդ ֆունկցիան միացված է շարունակական

“

Ինչ անել, եթե հանդիպեք անբաժանելի նման - հետ ընդմիջման կետինտեգրման միջակայքի վրա. Սա նշանակում է, որ օրինակում տառասխալ կա: (Ամենայն հավանականությամբ), կամ վերապատրաստման առաջադեմ մակարդակի մասին: Վերջին դեպքում պայմանավորված հավելումային հատկություններ, մենք պետք է դիտարկենք երկու անպատշաճ ինտեգրալ ընդմիջումներով և հետո զբաղվենք գումարով։

Երբեմն, տառասխալի կամ դիտավորության պատճառով, սխալ ինտեգրալը կարող է ընդհանրապես գոյություն չունի, այսպես, օրինակ, եթե դնենք վերը նշված ինտեգրալի հայտարարը Քառակուսի արմատ«x»-ից, ապա ինտեգրման միջակայքի մի մասն ընդհանրապես չի ներառվի ինտեգրացիայի սահմանման տիրույթում:

Ավելին, ոչ պատշաճ ինտեգրալը կարող է գոյություն չունենալ նույնիսկ ողջ «թվացյալ բարեկեցությամբ»: Դասական օրինակ. Չնայած կոսինուսի որոշակիությանը և շարունակականությանը, նման ոչ պատշաճ ինտեգրալ գոյություն չունի: Ինչո՞ւ։ Դա շատ պարզ է, քանի որ.
- գոյություն չունի համապատասխան սահմանաչափ.

Եվ նման օրինակներ, թեև հազվադեպ են, բայց գործնականում լինում են: Այսպիսով, ի լրումն կոնվերգենցիայի և տարաձայնությունների, կա նաև լուծման երրորդ արդյունքը վավերական պատասխանով. «ոչ պատշաճ ինտեգրալ չկա»:

Հարկ է նաև նշել, որ ոչ պատշաճ ինտեգրալի խիստ սահմանումը տրվում է հենց սահմանի միջոցով, և ցանկացողները կարող են ծանոթանալ դրան. ուսումնական գրականություն. Դե, մենք շարունակում ենք գործնական դասև անցեք ավելի բովանդակալից առաջադրանքների.

Օրինակ 3

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Նախ փորձենք գտնել հակաածանցյալ ֆունկցիան (անորոշ ինտեգրալ): Եթե ​​դա չկարողանանք, ապա բնականաբար չենք կարողանա լուծել նաև ոչ պատշաճ ինտեգրալը։

Աղյուսակային ինտեգրալներից որի՞ն է նման ինտեգրանդը: Դա ինձ հիշեցնում է արկտանգենս. . Այս նկատառումները հուշում են, որ լավ կլիներ հայտարարի մեջ ունենալ քառակուսի: Սա կատարվում է փոխարինման միջոցով:

Փոխարինենք.

Անորոշ ինտեգրալը գտնվել է այս դեպքում, անիմաստ է ավելացնել հաստատուն.

Միշտ օգտակար է ստուգել նախագիծը, այսինքն՝ տարբերակել ստացված արդյունքը.

Ստացվել է սկզբնական ինտեգրալը, ինչը նշանակում է, որ անորոշ ինտեգրալը ճիշտ է գտնվել։

Այժմ մենք գտնում ենք ոչ պատշաճ ինտեգրալը.

(1) Մենք լուծումը գրում ենք բանաձևի համաձայն . Ավելի լավ է անհապաղ տեղափոխել հաստատունը սահմանային նշանից այն կողմ, որպեսզի այն չխանգարի հետագա հաշվարկներին:

(2) Մենք փոխարինում ենք վերին և ստորին սահմանները Նյուտոն-Լայբնից բանաձևի համաձայն: Ինչո՞ւ ժամը ? Տե՛ս արկտանգենսի գրաֆիկը արդեն առաջարկված հոդվածում:

(3) Մենք ստանում ենք վերջնական պատասխանը: Փաստ, որն օգտակար է անգիր իմանալ.

Առաջադեմ ուսանողները կարող են առանձին չգտնել անորոշ ինտեգրալը և չօգտագործել փոխարինման մեթոդը, այլ օգտագործել ֆունկցիան դիֆերենցիալ նշանի տակ փոխարինելու և սխալ ինտեգրալը «անմիջապես» լուծելու մեթոդը: Այս դեպքում լուծումը պետք է նման լինի.

“

Ինտեգրանդը շարունակական է:

“

Օրինակ 4

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

! Սա տիպիկ օրինակ է, և նմանատիպ ինտեգրալներ շատ հաճախ են հանդիպում։ Լավ աշխատիր: Հակածանցյալ ֆունկցիան այստեղ կարելի է գտնել՝ օգտագործելով ամբողջական քառակուսի ընտրելու մեթոդը Որոշ կոտորակների ինտեգրում.

Օրինակ 5

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Այս ինտեգրալը կարելի է մանրամասն լուծել, այսինքն՝ սկզբում գտնել անորոշ ինտեգրալը՝ կատարելով փոփոխականի փոփոխություն։ Կամ կարող եք լուծել «անմիջապես»՝ ֆունկցիան դիֆերենցիալ նշանի տակ ներառելով: Ո՞վ ունի մաթեմատիկական պատրաստվածություն:

Դասի վերջում լրացրեք լուծումները և պատասխանները:

Ինտեգրման անսահման ստորին սահմանով ոչ պատշաճ ինտեգրալների լուծումների օրինակներ կարելի է գտնել էջում Ոչ պատշաճ ինտեգրալների լուծման արդյունավետ մեթոդներ. Այնտեղ մենք վերլուծեցինք նաև այն դեպքը, երբ ինտեգրման երկու սահմաններն էլ անսահման են։

Անսահմանափակ ֆունկցիաների ոչ պատշաճ ինտեգրալներ

Կամ երկրորդ տեսակի ոչ պատշաճ ինտեգրալներ. Երկրորդ տեսակի անպատշաճ ինտեգրալները նենգորեն «գաղտնագրվում» են սովորական որոշակի ինտեգրալի տակ և միանգամայն նույն տեսքն ունեն: Բայց, ի տարբերություն որոշյալ ինտեգրալիի, ինտեգրալը կրում է անսահման ընդհատում (չկա). 1) կետում, 2) կամ կետում, 3) կամ միանգամից երկու կետերում, 4) կամ նույնիսկ ինտեգրման հատվածում: Մենք կանդրադառնանք առաջին երկու դեպքերին հոդվածի վերջում 3-4 դեպքերի համար կա լրացուցիչ դասի հղում:

Պարզապես մի օրինակ պարզ դարձնելու համար. Թվում է, թե դա որոշակի ինտեգրալ է։ Բայց իրականում սա երկրորդ տեսակի ոչ պատշաճ ինտեգրալ է, եթե մենք ստորին սահմանի արժեքը փոխարինում ենք ինտեգրանդով, ապա մեր հայտարարը գնում է զրոյի, այսինքն՝ ինտեգրալն այս պահին պարզապես գոյություն չունի։

Ընդհանրապես, ոչ պատշաճ ինտեգրալը վերլուծելիս դուք միշտ պետք է փոխարինեք ինտեգրման երկու սահմանները ինտեգրման մեջ. Այս առումով, եկեք ստուգենք վերին սահմանը. . Այստեղ ամեն ինչ լավ է։

Քննարկվող ոչ պատշաճ ինտեգրալի տեսակի կորագիծ տրապիզոիդը սկզբունքորեն ունի հետևյալ տեսքը.

Այստեղ ամեն ինչ գրեթե նույնն է, ինչ առաջին տեսակի ինտեգրալում։

Մեր ինտեգրալը թվային է մակերեսին հավասարստվերավորված կոր trapezoid, որը սահմանափակված չէ վերևում: Այս դեպքում կարող է լինել երկու տարբերակ*՝ անպատշաճ ինտեգրալը շեղվում է (տարածքն անվերջ է) կամ անպատշաճ ինտեգրալը հավասար է վերջավոր թվի (այսինքն՝ անսահման գործչի մակերեսը վերջավոր է):

* լռելյայնորեն մենք սովորաբար ենթադրում ենք, որ ոչ պատշաճ ինտեգրալը գոյություն ունի

Մնում է միայն փոփոխել Նյուտոն-Լայբնից բանաձեւը։ Այն նույնպես փոփոխվում է սահմանի օգնությամբ, բայց սահմանն այլեւս չի ձգտում դեպի անսահմանություն, այլ դեպի աջ կողմում գտնվող արժեք:Գծագրից հեշտ է հետևել՝ առանցքի երկայնքով պետք է անսահման մոտենալ ճեղքման կետին աջ կողմում.

Տեսնենք, թե ինչպես է դա իրականացվում գործնականում:

Օրինակ 6

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Ինտեգրանդը որոշակի կետում ունի անսահման ընդհատում (մի մոռացեք բանավոր կամ սևագրի վրա ստուգել, ​​որ ամեն ինչ կարգին է վերին սահմանի հետ):

Նախ, եկեք հաշվարկենք անորոշ ինտեգրալը.

Փոխարինում:

Եթե ​​փոխարինման հետ կապված որևէ դժվարություն ունեք, դիմեք դասին Փոխարինման մեթոդ անորոշ ինտեգրալում.

Եկեք հաշվարկենք ոչ պատշաճ ինտեգրալը.

(1) Ի՞նչ նորություն կա այստեղ: Լուծման տեխնոլոգիայի առումով գործնականում ոչինչ չկա։ Միակ բանը, որ փոխվել է, սահմանաչափի պատկերակի տակ մուտքն է՝ . Հավելումը նշանակում է, որ մենք ձգտում ենք դեպի աջ կողմում գտնվող արժեքը (ինչը տրամաբանական է. տես գրաֆիկը): Նման սահմանը սահմանների տեսության մեջ կոչվում է միակողմանի սահմանափակում. Այս դեպքում ունենք աջ ձեռքի սահմանը.

(2) Մենք փոխարինում ենք վերին և ստորին սահմանները՝ օգտագործելով Newton-Leibniz բանաձևը:

(3) Եկեք զբաղվենք . Ինչպե՞ս որոշել, թե ուր է գնում արտահայտությունը: Կոպիտ ասած, պարզապես պետք է արժեքը փոխարինել դրա մեջ, փոխարինել երեք քառորդով և նշել, որ . Եկեք սանրենք պատասխանը.

Այս դեպքում ոչ պատշաճ ինտեգրալը հավասար է բացասական թվի։ Սրանում հանցագործություն չկա, ուղղակի առանցքի տակ է գտնվում համապատասխան կոր trapezoid-ը։

Եվ հիմա երկու օրինակ անկախ լուծումների համար.

Օրինակ 7

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Օրինակ 8

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Եթե ​​կետում ինտեգրանդը գոյություն չունի

Նման անպատշաճ ինտեգրալի համար անսահման կոր trapezoid սկզբունքորեն այսպիսի տեսք ունի.

Անպատշաճ ինտեգրալ՝ անսահման ինտեգրման սահմանաչափով

Երբեմն նման ոչ պատշաճ ինտեգրալն անվանում են նաև առաջին տեսակի ոչ պատշաճ ինտեգրալ..gif" width="49" height="19 src=">։

Ավելի քիչ տարածված են անվերջ ստորին սահմանով կամ երկու անսահման սահմաններով ինտեգրալները.

Մենք կդիտարկենք ամենատարածված դեպքը https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Ոչ միշտ չէ: Ինտեգրանդhttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">

Եկեք գծագրում պատկերենք ինտեգրանդ ֆունկցիայի գրաֆիկը։ Տիպիկ գրաֆիկը և կոր trapezoid-ը այս դեպքի համար ունի հետևյալ տեսքը.

Անպատշաճ ինտեգրալhttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">», այսինքն՝ տարածքն էլ է անսահման։ Կարող է այդպես լինել։Այս դեպքում ասում են, որ ոչ պատշաճ ինտեգրալը տարբերվում է.

2) Բայց. Որքան էլ պարադոքսալ հնչի, անսահման թվի մակերեսը կարող է հավասար լինել… վերջավոր թվի: Օրինակ՝ .. Երկրորդ դեպքում ոչ պատշաճ ինտեգրալը համընկնում է.

Ի՞նչ է պատահում, եթե առանցքից ներքև գտնվի անսահման կոր տրապիզոիդ:.gif" width="217" height="51 src=">:

: .

Օրինակ 1

Ինտեգրանդ ֆունկցիան https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, ինչը նշանակում է, որ ամեն ինչ կարգին է, և սխալ ինտեգրալը կարելի է հաշվարկել օգտագործելով « ստանդարտ» մեթոդը:

Մեր բանաձևի կիրառումը https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">

Այսինքն, ոչ պատշաճ ինտեգրալը շեղվում է, և ստվերավորված կոր trapezoid-ի մակերեսը հավասար է անսահմանության:

Անպատշաճ ինտեգրալներ լուծելիս շատ կարևոր է իմանալ, թե ինչ տեսք ունեն հիմնական տարրական ֆունկցիաների գրաֆիկները:

Օրինակ 2

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Եկեք նկարենք.

Նախ, մենք նշում ենք հետևյալը. ինտեգրանդը շարունակական է կիսամյակային միջակայքում: Լավ..gif" width="327" height="53">

(1) Մենք վերցնում ենք հզորության ֆունկցիայի ամենապարզ ինտեգրալը (այս հատուկ դեպքը շատ աղյուսակներում է): Ավելի լավ է մինուս նշանը անմիջապես տեղափոխել սահմանային նշանից այն կողմ, որպեսզի հետագա հաշվարկներում այն ​​չխանգարի։

(2) Մենք փոխարինում ենք վերին և ստորին սահմանները՝ օգտագործելով Newton-Leibniz բանաձևը:

(3) Մենք նշում ենք, որ https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Պարոնայք, սա վաղուց պետք է հասկանալ. ) և պարզեցնել պատասխանը:

Այստեղ անսահման կոր trapezoid-ի մակերեսը վերջավոր թիվ է: Անհավատալի, բայց իրական.

Օրինակ 3

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Ինտեգրանդը շարունակական է:

Նախ փորձենք գտնել հակաածանցյալ ֆունկցիան (անորոշ ինտեգրալ):

Աղյուսակային ինտեգրալներից որի՞ն է նման ինտեգրանդը: Դա ինձ հիշեցնում է արկտանգենս. . Այս նկատառումները հուշում են, որ լավ կլիներ հայտարարի մեջ ունենալ քառակուսի: Սա կատարվում է փոխարինման միջոցով:

Փոխարինենք.

Միշտ օգտակար է ստուգում կատարել, այսինքն՝ տարբերակել ստացված արդյունքը.

Այժմ մենք գտնում ենք ոչ պատշաճ ինտեգրալը.

(1) Մենք լուծումը գրում ենք բանաձևի համաձայն . Ավելի լավ է անհապաղ տեղափոխել հաստատունը սահմանային նշանից այն կողմ, որպեսզի այն չխանգարի հետագա հաշվարկներին:

(2) Մենք փոխարինում ենք վերին և ստորին սահմանները՝ համաձայն Newton-Leibniz բանաձևի..gif" width="56" height="19 src=">: Տես արկտանգենս գրաֆիկը արդեն բազմիցս առաջարկվող հոդվածում:

(3) Մենք ստանում ենք վերջնական պատասխանը: Փաստ, որն օգտակար է անգիր իմանալ.

Առաջադեմ ուսանողները կարող են առանձին չգտնել անորոշ ինտեգրալը և չօգտագործել փոխարինման մեթոդը, այլ օգտագործել ֆունկցիան դիֆերենցիալ նշանի տակ փոխարինելու և սխալ ինտեգրալը «անմիջապես» լուծելու մեթոդը: Այս դեպքում լուծումը պետք է նման լինի.

“

Ինտեգրանդ ֆունկցիան շարունակական է՝ https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“

Օրինակ 4

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

! Սա տիպիկ օրինակ է, և նմանատիպ ինտեգրալներ շատ հաճախ են հանդիպում։ Լավ աշխատիր: Հակածանցյալ ֆունկցիան հայտնաբերվում է այստեղ՝ օգտագործելով ամբողջական քառակուսի մեկուսացման մեթոդը:

Օրինակ 5

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Այս ինտեգրալը կարելի է մանրամասն լուծել, այսինքն՝ սկզբում գտնել անորոշ ինտեգրալը՝ կատարելով փոփոխականի փոփոխություն։ Կամ կարող եք լուծել այն «անմիջապես»՝ ֆունկցիան դիֆերենցիալ նշանի տակ դնելով:

Անսահմանափակ ֆունկցիաների ոչ պատշաճ ինտեգրալներ

Երբեմն նման ոչ պատշաճ ինտեգրալները կոչվում են երկրորդ տեսակի ոչ պատշաճ ինտեգրալներ: Երկրորդ տեսակի ոչ պատշաճ ինտեգրալները նենգորեն «գաղտնագրվում են» սովորական որոշակի ինտեգրալի տակ և միանգամայն նույն տեսքն ունեն՝ ..gif" width="39" height="15 src=">, 2) կամ կետում, 3) կամ միանգամից երկու կետերում, 4) կամ նույնիսկ ինտեգրման հատվածի վերաբերյալ, մենք կքննարկենք առաջին երկու դեպքերը հոդվածի վերջում:

Պարզապես մի օրինակ պարզ դարձնելու համար՝ https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, ապա մեր հայտարարը գնում է զրոյի այսինքն՝ ինտեգրանդն այս պահին պարզապես գոյություն չունի։

Ընդհանրապես, ոչ պատշաճ ինտեգրալը վերլուծելիս դուք միշտ պետք է փոխարինեք ինտեգրման երկու սահմանները ինտեգրման մեջ..jpg" alt="Անպատշաճ ինտեգրալ, ընդհատման կետ ինտեգրման ստորին սահմանում" width="323" height="380">!}

Այստեղ ամեն ինչ գրեթե նույնն է, ինչ առաջին տեսակի ինտեգրալում։
Մեր ինտեգրալը թվայինորեն հավասար է ստվերավորված կոր trapezoid-ի մակերեսին, որը սահմանափակված չէ վերևից: Այս դեպքում կարող է լինել երկու տարբերակ՝ անպատշաճ ինտեգրալը շեղվում է (տարածքն անվերջ է) կամ անպատշաճ ինտեգրալը հավասար է վերջավոր թվի (այսինքն՝ անսահման գործչի մակերեսը վերջավոր է):

Մնում է միայն փոփոխել Նյուտոն-Լայբնից բանաձեւը։ Այն նույնպես փոփոխվում է սահմանի օգնությամբ, բայց սահմանն այլեւս չի ձգտում դեպի անսահմանություն, այլ արժեւորելhttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> աջ կողմում.

Օրինակ 6

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Ինտեգրանդը որոշակի կետում ունի անսահման ընդհատում (մի մոռացեք բանավոր կամ սևագրի վրա ստուգել, ​​որ ամեն ինչ կարգին է վերին սահմանի հետ):

Նախ, եկեք հաշվարկենք անորոշ ինտեգրալը.

Փոխարինում:

Եկեք հաշվարկենք ոչ պատշաճ ինտեգրալը.

(1) Ի՞նչ նորություն կա այստեղ: Լուծման տեխնոլոգիայի առումով գործնականում ոչինչ չկա։ Միակ բանը, որ փոխվել է, սահմանաչափի պատկերակի տակ մուտքն է՝ . Հավելումը նշանակում է, որ մենք ձգտում ենք դեպի աջ կողմում գտնվող արժեքը (ինչը տրամաբանական է. տես գրաֆիկը): Նման սահմանը սահմանների տեսության մեջ կոչվում է միակողմանի սահման: Այս դեպքում մենք ունենք աջակողմյան սահման:

(2) Մենք փոխարինում ենք վերին և ստորին սահմանները՝ օգտագործելով Newton-Leibniz բանաձևը:

(3) Եկեք հասկանանք https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">: Ինչպե՞ս որոշել, թե արտահայտությունը ուր պետք է գնա, կոպիտ ասած. , դուք պարզապես պետք է փոխարինեք արժեքը, փոխարինեք երեք քառորդով և նշեք, որ սանրել պատասխանը:

Այս դեպքում ոչ պատշաճ ինտեգրալը հավասար է բացասական թվի։

Օրինակ 7

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Օրինակ 8

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը:

Եթե ​​կետում ինտեգրանդը գոյություն չունի

Նման անպատշաճ ինտեգրալի համար անսահման կոր trapezoid-ը սկզբունքորեն ունի հետևյալ տեսքը.

Այստեղ ամեն ինչ բացարձակապես նույնն է, միայն թե մեր սահմանը հակված է արժեւորելhttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> մենք պետք է անսահման մոտենանք բեկման կետին. ձախ.

Որոշակի ինտեգրալ՝ որպես ինտեգրալ գումարի սահման

կարող է գոյություն ունենալ (այսինքն ունենալ որոշակի վերջնական արժեք) միայն այն դեպքում, եթե առկա են պայմանները

Եթե ​​այս պայմաններից գոնե մեկը խախտվում է, ապա սահմանումը կորցնում է իր իմաստը։ Իրոք, անսահման հատվածի դեպքում, օրինակ, [ ա; ) այն չի կարելի բաժանել Պվերջավոր երկարությամբ մասեր
, որը, ընդ որում, սեգմենտների քանակի ավելացման դեպքում կձգտի զրոյի։ Ինչ-որ պահի անսահմանափակության դեպքում Հետ[ա; բ] կետի կամայական ընտրության պահանջը խախտված է մասնակի հատվածների վրա – չի կարող ընտրվել =Հետ, քանի որ այս պահին ֆունկցիայի արժեքը որոշված ​​չէ: Այնուամենայնիվ, նույնիսկ այս դեպքերի համար հնարավոր է ընդհանրացնել որոշակի ինտեգրալի հասկացությունը՝ սահմանին մեկ այլ հատված ներմուծելով։ Անվերջ ինտերվալների և ընդհատվող (անսահմանափակ) ֆունկցիաների վրա ինտեգրալները կոչվում են ոչ քոնը.

Սահմանում.

Թողեք գործառույթը
սահմանվում է միջակայքում [ ա; ) և ինտեգրելի է ցանկացած վերջավոր միջակայքում [ ա; բ], այսինքն. գոյություն ունի
որեւէ մեկի համար բ > ա. Տիպի սահմանափակում
կանչեց ոչ պատշաճ ինտեգրալ առաջին տեսակ (կամ անպատշաճ ինտեգրալ անսահման միջակայքում) և նշանակել
.

Այսպիսով, ըստ սահմանման,
=
.

Եթե ​​աջ կողմի սահմանը գոյություն ունի և վերջավոր է, ապա ոչ պատշաճ ինտեգրալը
կանչեց կոնվերգենտ . Եթե ​​այս սահմանը անսահման է, կամ ընդհանրապես գոյություն չունի, ապա ասում են, որ ոչ պատշաճ ինտեգրալը տարբերվում է .

Նմանապես, մենք կարող ենք ներկայացնել ֆունկցիայի ոչ պատշաճ ինտեգրալի հայեցակարգը
ընդմիջումով (–; բ]:

=
.

Եվ ֆունկցիայի ոչ պատշաճ ինտեգրալը
ընդմիջումով (–; +) սահմանվում է որպես վերը ներկայացված ինտեգրալների գումար.

=
+
,

Որտեղ Ա- կամայական կետ. Այս ինտեգրալը համընկնում է, եթե երկու տերմիններն էլ համընկնում են, և շեղվում է, եթե տերմիններից գոնե մեկը շեղվում է:

Երկրաչափական տեսանկյունից ինտեգրալը
,
, որոշում է ֆունկցիայի գրաֆիկով վերևում սահմանափակված անվերջ կորագիծ տրապիզոնի տարածքի թվային արժեքը
, ձախ – ուղիղ
, ներքևից՝ OX առանցքով։ Ինտեգրալի կոնվերգենցիան նշանակում է նման տրապիզոնի վերջավոր տարածքի առկայություն և դրա հավասարությունը շարժական աջ պատով կորագիծ տրապիզոնի տարածքի սահմանին:
.

Անսահման սահման ունեցող ինտեգրալի դեպքում կարող ենք ընդհանրացնել Նյուտոն-Լայբնից բանաձև:

=
=F( + ) – F( ա),

որտեղ F( + ) =
. Եթե ​​այս սահմանը գոյություն ունի, ապա ինտեգրալը համընկնում է, հակառակ դեպքում այն ​​շեղվում է:

Մենք դիտարկեցինք որոշակի ինտեգրալի հասկացության ընդհանրացումը անսահման միջակայքի դեպքին:

Այժմ դիտարկենք ընդհանրացում անսահմանափակ ֆունկցիայի դեպքի համար:

Սահմանում

Թողեք գործառույթը
սահմանվում է միջակայքում [ ա; բ), անսահմանափակ է կետի որոշ հարևանությամբ բ, և շարունակական է ցանկացած միջակայքում
, որտեղ>0 (և, հետևաբար, ինտեգրելի է այս միջակայքում, այսինքն.
գոյություն ունի): Տիպի սահմանափակում
կանչեց երկրորդ տեսակի ոչ պատշաճ ինտեգրալ (կամ անսահմանափակ ֆունկցիայի ոչ պատշաճ ինտեգրալ) և նշվում է
.

Այսպիսով, կետում անսահմանափակի ոչ պատշաճ ինտեգրալը բգործառույթները գոյություն ունեն ըստ սահմանման

=
.

Եթե ​​աջ կողմի սահմանը գոյություն ունի և վերջավոր է, ապա կոչվում է ինտեգրալ կոնվերգենտ. Եթե ​​չկա վերջավոր սահման, ապա կոչվում է ոչ պատշաճ ինտեգրալ տարբերվող.

Նմանապես, մենք կարող ենք սահմանել ֆունկցիայի ոչ պատշաճ ինտեգրալը
կետում ունենալով անսահման ընդհատում Ա:

=
.

Եթե ​​ֆունկցիան
ներքին կետում ունի անսահման ընդհատում Հետ
, ապա ոչ պատշաճ ինտեգրալը սահմանվում է հետևյալ կերպ

=
+
=
+
.

Այս ինտեգրալը համընկնում է, եթե երկու տերմիններն էլ համընկնում են, և շեղվում է, եթե առնվազն մեկ անդամ շեղվում է:

Երկրաչափական տեսանկյունից անսահմանափակ ֆունկցիայի ոչ պատշաճ ինտեգրալը բնութագրում է նաև անսահմանափակ կոր trapezoid-ի տարածքը.

Քանի որ ոչ պատշաճ ինտեգրալը ստացվում է որոշակի ինտեգրալից սահմանին անցնելով, որոշ ինտեգրալի բոլոր հատկությունները կարող են փոխանցվել (համապատասխան ճշգրտումներով) առաջին և երկրորդ տեսակի ոչ պատշաճ ինտեգրալներին:

Շատ խնդիրներում, որոնք հանգեցնում են ոչ պատշաճ ինտեգրալների, պետք չէ իմանալ, թե ինչի է հավասար այս ինտեգրալը, բավական է միայն ստուգել դրա սերտաճումը կամ տարաձայնությունը։ Դրա համար նրանք օգտագործում են կոնվերգենցիայի նշաններ. Անպատշաճ ինտեգրալների կոնվերգենցիայի նշաններ.

1) Համեմատության նշան.

Թող դա լինի բոլորի համար X

. Հետո եթե
համընկնում է, հետո զուգակցվում
, և

. Եթե
շեղվում է, ապա շեղվում և
.

2) Եթե համընկնում է
, ապա համընկնում է և
(վերջին ինտեգրալն այս դեպքում կոչվում է բացարձակապես կոնվերգենտ).

Անսահմանափակ ֆունկցիաների ոչ պատշաճ ինտեգրալների կոնվերգենցիայի և տարաձայնության նշանները նման են վերը ձևակերպվածներին:

Խնդիրների լուծման օրինակներ.

Օրինակ 1.

Ա)
; բ)
; V)

G)
; դ)
.

Լուծում.

ա) Ըստ սահմանման մենք ունենք.

.

բ) Նույն կերպ

Հետևաբար, այս ինտեգրալը համընկնում է և հավասար է .

գ) ըստ սահմանման
=
+
, և Ա- կամայական համար: Եկեք մեր գործի մեջ դնենք
, ապա մենք ստանում ենք.

Այս ինտեգրալը համընկնում է:

Սա նշանակում է, որ այս ինտեգրալը տարբերվում է:

ե) Դիտարկենք
. Ինտեգրանդի հակաածանցյալը գտնելու համար անհրաժեշտ է կիրառել ըստ մասերի ինտեգրման մեթոդը։ Այնուհետև մենք ստանում ենք.

Քանի որ ոչ մեկը
, ոչ էլ
գոյություն չունեն, ապա չկա և

Հետևաբար, այս ինտեգրալը տարբերվում է:

Օրինակ 2.

Ուսումնասիրեք ինտեգրալի կոնվերգենցիան կախված Պ.

Լուծում.

ժամը
մենք ունենք:

Եթե
, Դա
Եվ. Հետևաբար, ինտեգրալը տարբերվում է:

Եթե
, Դա
, Ա
, Հետո

=,

Հետևաբար, ինտեգրալը համընկնում է:

Եթե
, Դա

հետևաբար, ինտեգրալը տարբերվում է:

Այսպիսով,

Օրինակ 3.

Հաշվեք ոչ պատշաճ ինտեգրալը կամ հաստատեք դրա տարբերությունը.

Ա)
; բ)
; V)
.

Լուծում.

ա) Ինտեգրալ
երկրորդ տեսակի ոչ պատշաճ ինտեգրալ է, քանի որ ինտեգրանդը
ոչ մի կետով սահմանափակված

. Այնուհետև, ըստ սահմանման,

.

Ինտեգրալը համընկնում է և հավասար է .

բ) Հաշվի առեք
. Այստեղ նույնպես ինտեգրանդը սահմանափակված չէ կետում
. Հետևաբար, այս ինտեգրալը երկրորդ տեսակի անպատշաճ է և, ըստ սահմանման,

Հետևաբար, ինտեգրալը տարբերվում է:

գ) Հաշվի առեք
. Ինտեգրանդ
անսահման բաց է ունենում երկու կետում.
Եվ
, որոնցից առաջինը պատկանում է ինտեգրման միջակայքին
. Հետևաբար, այս ինտեգրալը երկրորդ կարգի ոչ պատշաճ ինտեգրալ է։ Հետո, ըստ սահմանման

=

=

.

Հետևաբար, ինտեգրալը համընկնում է և հավասար է
.