Yksityisyytesi säilyttäminen on meille tärkeää. Tästä syystä olemme kehittäneet tietosuojakäytännön, joka kuvaa kuinka käytämme ja säilytämme tietojasi. Tutustu tietosuojakäytäntöihimme ja kerro meille, jos sinulla on kysyttävää.

Henkilötietojen kerääminen ja käyttö

Henkilötiedoilla tarkoitetaan tietoja, joiden avulla voidaan tunnistaa tietty henkilö tai ottaa häneen yhteyttä.

Sinua voidaan pyytää antamaan henkilötietosi milloin tahansa, kun otat meihin yhteyttä.

Alla on esimerkkejä siitä, minkä tyyppisistä henkilötiedoista saatamme kerätä ja kuinka voimme käyttää tällaisia ​​tietoja.

Mitä henkilötietoja keräämme:

• Kun lähetät pyynnön sivustolla, voimme kerätä erilaisia ​​tietoja, kuten nimesi, puhelinnumerosi, osoitteesi sähköposti jne.

Kuinka käytämme henkilötietojasi:

• Meidän keräämä henkilökohtaisia ​​tietoja avulla voimme ottaa sinuun yhteyttä ja tiedottaa ainutlaatuisista tarjouksista, kampanjoista ja muista tapahtumista ja tulevista tapahtumista.
• Ajoittain voimme käyttää henkilötietojasi tärkeiden ilmoitusten ja viestien lähettämiseen.
• Saatamme myös käyttää henkilötietoja sisäisiin tarkoituksiin, kuten auditointiin, data-analyysiin ja erilaisiin tutkimuksiin parantaaksemme tarjoamiamme palveluita ja tarjotaksemme sinulle palveluitamme koskevia suosituksia.
• Jos osallistut arvontaan, kilpailuun tai vastaavaan promootioon, voimme käyttää antamiasi tietoja tällaisten ohjelmien hallinnointiin.

Tietojen luovuttaminen kolmansille osapuolille

Emme luovuta sinulta saatuja tietoja kolmansille osapuolille.

Poikkeukset:

• Tarvittaessa - lain, oikeudenkäyntimenettelyn, oikeudenkäynnin ja/tai julkisten pyyntöjen tai pyynnön perusteella valtion virastot Venäjän federaation alueella - paljasta henkilötietosi. Saatamme myös paljastaa tietoja sinusta, jos katsomme, että tällainen paljastaminen on tarpeellista tai tarkoituksenmukaista turvallisuus-, lainvalvonta- tai muihin yleisiin tarkoituksiin liittyvistä syistä.
• Uudelleenjärjestelyn, sulautumisen tai myynnin yhteydessä voimme siirtää keräämämme henkilötiedot sovellettavalle seuraajalle kolmannelle osapuolelle.

Henkilötietojen suojaaminen

Ryhdymme varotoimiin - mukaan lukien hallinnolliset, tekniset ja fyysiset - henkilötietojesi suojaamiseksi katoamiselta, varkaudelta ja väärinkäytöltä sekä luvattomalta käytöltä, paljastamiselta, muuttamiselta ja tuhoutumiselta.

Yksityisyytesi kunnioittaminen yritystasolla

Varmistaaksemme, että henkilötietosi ovat turvassa, välitämme tietosuoja- ja turvallisuusstandardit työntekijöillemme ja noudatamme tiukasti tietosuojakäytäntöjä.

Yhtälöiden ja epäyhtälöiden ratkaiseminen moduulilla aiheuttaa usein vaikeuksia. Jos kuitenkin ymmärrät hyvin mistä on kyse lukumoduuli, Ja kuinka moduulimerkin sisältäviä lausekkeita laajennetaan oikein, sitten läsnäolo yhtälössä lauseke moduulimerkin alla, lakkaa olemasta este sen ratkaisulle.

Vähän teoriaa. Jokaisella numerolla on kaksi ominaisuutta: luvun itseisarvo ja sen etumerkki.

Esimerkiksi numerolla +5 tai yksinkertaisesti 5 on "+"-merkki ja absoluuttinen arvo 5.

Numerolla -5 on "-"-merkki ja absoluuttinen arvo 5.

Numeroiden 5 ja -5 absoluuttiset arvot ovat 5.

Luvun x itseisarvoa kutsutaan luvun moduuliksi ja sitä merkitään |x|.

Kuten näemme, luvun moduuli on yhtä suuri kuin itse luku, jos tämä luku on suurempi tai yhtä suuri kuin nolla, ja tämä luku, jolla on päinvastainen etumerkki, jos tämä luku on negatiivinen.

Sama koskee kaikkia lausekkeita, jotka näkyvät moduulimerkin alla.

Moduulin laajennussääntö näyttää tältä:

|f(x)|= f(x), jos f(x) ≥ 0, ja

|f(x)|= - f(x), jos f(x)< 0

Esimerkiksi |x-3|=x-3, jos x-3≥0 ja |x-3|=-(x-3)=3-x, jos x-3<0.

Jotta voit ratkaista yhtälön, joka sisältää lausekkeen moduulimerkin alla, sinun on ensin laajentaa moduulia moduulin laajennussäännön mukaisesti.

Sitten yhtälöstämme tai epäyhtälöstämme tulee kahdeksi eri yhtälöksi kahdella eri numeerisella aikavälillä.

Numeerisella välillä on yksi yhtälö, jolla moduulimerkin alla oleva lauseke on ei-negatiivinen.

Ja toinen yhtälö on olemassa välissä, jolla moduulimerkin alla oleva lauseke on negatiivinen.

Katsotaanpa yksinkertaista esimerkkiä.

Ratkaistaan ​​yhtälö:

|x-3|=-x 2 +4x-3

1. Avataan moduuli.

|x-3|=x-3, jos x-3≥0, ts. jos x≥3

|x-3|=-(x-3)=3-x, jos x-3<0, т.е. если х<3

2. Saimme kaksi numeerista väliä: x≥3 ja x<3.

Tarkastellaan, mihin yhtälöihin alkuperäinen yhtälö on muunnettu kullakin aikavälillä:

A) Kun x≥3 |x-3|=x-3, ja haavamme on muotoa:

Huomio! Tämä yhtälö on olemassa vain välillä x≥3!

Avataan sulut ja esitellään samanlaiset termit:

ja ratkaise tämä yhtälö.

Tällä yhtälöllä on juuret:

x 1 = 0, x 2 = 3

Huomio! koska yhtälö x-3=-x 2 +4x-3 on olemassa vain välillä x≥3, olemme kiinnostuneita vain niistä juurista, jotka kuuluvat tähän väliin. Tämä ehto täyttyy vain x 2 =3.

B) Kohdassa x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

Huomio! Tämä yhtälö on olemassa vain välillä x<3!

Avataan sulut ja esitellään samanlaiset termit. Saamme yhtälön:

x 1 = 2, x 2 = 3

Huomio! koska yhtälö 3-x=-x 2 +4x-3 on olemassa vain välillä x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

Joten: ensimmäisestä intervallista otamme vain juuren x=3, toisesta juuren x=2.

Emme valitse matematiikkaa hänen ammattinsa, ja hän valitsee meidät.

Venäläinen matemaatikko Yu.I. Manin

Yhtälöt moduulilla

Koulumatematiikan vaikeimpia ratkaistavia ongelmia ovat yhtälöt, jotka sisältävät muuttujia moduulimerkin alla. Tällaisten yhtälöiden ratkaisemiseksi onnistuneesti sinun on tiedettävä moduulin määritelmä ja perusominaisuudet. Luonnollisesti opiskelijoilla on oltava taidot ratkaista tämän tyyppisiä yhtälöitä.

Peruskäsitteet ja ominaisuudet

Reaaliluvun moduuli (absoluuttinen arvo). merkitty ja se määritellään seuraavasti:

Moduulin yksinkertaiset ominaisuudet sisältävät seuraavat suhteet:

Huomaa, että kaksi viimeistä ominaisuutta pätevät mille tahansa parilliselle asteelle.

Lisäksi jos, missä, sitten ja

Monimutkaisemmat moduuliominaisuudet, joita voidaan käyttää tehokkaasti ratkaistaessa yhtälöitä moduuleilla, muotoillaan seuraavien lauseiden avulla:

Lause 1.Kaikille analyyttisille toiminnoille Ja eriarvoisuus on totta

Lause 2. Tasa-arvo vastaa eriarvoisuutta.

Lause 3. Tasa-arvo vastaa eriarvoisuutta.

Katsotaanpa tyypillisiä esimerkkejä ongelmien ratkaisemisesta aiheesta "Yhtälöt, jotka sisältävät muuttujia moduulimerkin alla."

Yhtälöiden ratkaiseminen moduulilla

Koulumatematiikan yleisin menetelmä yhtälöiden ratkaisemiseksi moduulilla on menetelmä, moduulin laajennuksen perusteella. Tämä menetelmä on universaali, sen käyttö voi kuitenkin yleensä johtaa erittäin hankalia laskelmiin. Tässä suhteessa opiskelijoiden tulisi tietää muita, tehokkaampia menetelmiä ja tekniikoita tällaisten yhtälöiden ratkaisemiseksi. Erityisesti, tarvitaan taitoja soveltaa lauseita, annettu tässä artikkelissa.

Esimerkki 1. Ratkaise yhtälö. (1)

Ratkaisu. Ratkaisemme yhtälön (1) käyttämällä "klassista" menetelmää - moduulien paljastamismenetelmää. Tätä varten jaetaan numeroakseli pisteitä ja väliajoiksi ja harkitse kolmea tapausta.

1. Jos , niin , , ja yhtälö (1) saa muodon . Tästä seuraa. Tästä syystä löydetty arvo ei kuitenkaan ole yhtälön (1) juuri.

2. Jos, sitten yhtälöstä (1) saadaan tai .

Siitä lähtien yhtälön (1) juuri.

3. Jos, sitten yhtälö (1) saa muodon tai . Huomioikaa se.

Vastaus: ,.

Kun ratkaisemme myöhempiä yhtälöitä moduulilla, hyödynnämme aktiivisesti moduulien ominaisuuksia tällaisten yhtälöiden ratkaisemisen tehokkuuden lisäämiseksi.

Esimerkki 2. Ratkaise yhtälö.

Ratkaisu. Siitä lähtien ja sitten yhtälöstä se seuraa. Tältä osin,,, ja yhtälö saa muodon. Täältä saamme. kuitenkin , siksi alkuperäisellä yhtälöllä ei ole juuria.

Vastaus: ei juuria.

Esimerkki 3. Ratkaise yhtälö.

Ratkaisu. Siitä lähtien. Jos, niin ja yhtälö saa muodon.

Täältä saamme.

Esimerkki 4. Ratkaise yhtälö.

Ratkaisu.Kirjoitetaan yhtälö uudelleen vastaavaan muotoon. (2)

Tuloksena oleva yhtälö kuuluu tyyppisiin yhtälöihin.

Kun otetaan huomioon Lause 2, voidaan väittää, että yhtälö (2) vastaa epäyhtälöä . Täältä saamme.

Vastaus:.

Esimerkki 5. Ratkaise yhtälö.

Ratkaisu. Tällä yhtälöllä on muoto. Siksi, Lauseen 3 mukaan, täällä on eriarvoisuutta tai .

Esimerkki 6. Ratkaise yhtälö.

Ratkaisu. Oletetaan, että. Koska , sitten annettu yhtälö saa toisen asteen yhtälön muodon, (3)

Jossa . Koska yhtälöllä (3) on yksi positiivinen juuri ja sitten . Tästä saamme kaksi alkuperäisen yhtälön juuria: Ja .

Esimerkki 7. Ratkaise yhtälö. (4)

Ratkaisu. Yhtälöstä lähtienvastaa kahden yhtälön yhdistelmää: ja , silloin yhtälöä (4) ratkaistaessa on tarkasteltava kahta tapausta.

1. Jos , niin tai .

Täältä saamme , ja .

2. Jos , niin tai .

Siitä lähtien.

Vastaus: , , , .

Esimerkki 8.Ratkaise yhtälö . (5)

Ratkaisu. Siitä lähtien ja sitten . Tästä ja yhtälöstä (5) seuraa, että ja , so. tässä meillä on yhtälöjärjestelmä

Tämä yhtälöjärjestelmä on kuitenkin epäjohdonmukainen.

Vastaus: ei juuria.

Esimerkki 9. Ratkaise yhtälö. (6)

Ratkaisu. Jos merkitsemme , niin ja yhtälöstä (6) saadaan

Tai . (7)

Koska yhtälöllä (7) on muoto , tämä yhtälö vastaa epäyhtälöä . Täältä saamme. Siitä lähtien tai .

Vastaus:.

Esimerkki 10.Ratkaise yhtälö. (8)

Ratkaisu.Lauseen 1 mukaan voimme kirjoittaa

(9)

Ottaen huomioon yhtälön (8) päätämme, että molemmat epäyhtälöt (9) muuttuvat yhtäläisiksi, ts. on yhtälöjärjestelmä

Lauseen 3 mukaan yllä oleva yhtälöjärjestelmä on kuitenkin sama kuin epäyhtälöjärjestelmä

(10)

Ratkaisemalla epäyhtälöjärjestelmä (10) saamme . Koska epäyhtälöjärjestelmä (10) vastaa yhtälöä (8), alkuperäisellä yhtälöllä on yksi juuri.

Vastaus:.

Esimerkki 11. Ratkaise yhtälö. (11)

Ratkaisu. Antaa ja , sitten yhtälö seuraa yhtälöstä (11).

Siitä seuraa, että ja . Tässä meillä on siis epätasa-arvojärjestelmä

Ratkaisu tähän eriarvoisuusjärjestelmään on Ja .

Vastaus: ,.

Esimerkki 12.Ratkaise yhtälö. (12)

Ratkaisu. Yhtälö (12) ratkaistaan ​​moduulien peräkkäisen laajentamisen menetelmällä. Tätä varten tarkastellaan useita tapauksia.

1. Jos , niin .

1.1. Jos , sitten ja , .

1.2. Jos, niin. kuitenkin , siksi tässä tapauksessa yhtälöllä (12) ei ole juuria.

2. Jos , niin .

2.1. Jos , sitten ja , .

2.2. Jos , sitten ja .

Vastaus: , , , , .

Esimerkki 13.Ratkaise yhtälö. (13)

Ratkaisu. Koska yhtälön (13) vasen puoli on ei-negatiivinen, niin . Tässä suhteessa ja yhtälö (13)

ottaa muodon tai .

Tiedetään, että yhtälö vastaa kahden yhtälön yhdistelmää ja , jonka saamme ratkaisemaan, . Koska , niin yhtälöllä (13) on yksi juuri.

Vastaus:.

Esimerkki 14. Ratkaise yhtälöjärjestelmä (14)

Ratkaisu. Siitä lähtien ja , sitten ja . Näin ollen yhtälöjärjestelmästä (14) saadaan neljä yhtälöjärjestelmää:

Yllä olevien yhtälöjärjestelmien juuret ovat yhtälöjärjestelmän (14) juuret.

Vastaus: ,, , , , , , .

Esimerkki 15. Ratkaise yhtälöjärjestelmä (15)

Ratkaisu. Siitä lähtien. Tässä suhteessa yhtälöjärjestelmästä (15) saadaan kaksi yhtälöjärjestelmää

Ensimmäisen yhtälöjärjestelmän juuret ovat ja , ja toisesta yhtälöjärjestelmästä saamme ja .

Vastaus: , , , .

Esimerkki 16. Ratkaise yhtälöjärjestelmä (16)

Ratkaisu. Järjestelmän (16) ensimmäisestä yhtälöstä seuraa, että .

Siitä lähtien . Tarkastellaan järjestelmän toista yhtälöä. Koska, Se, ja yhtälö saa muodon, , tai .

Jos korvaat arvonjärjestelmän (16) ensimmäiseen yhtälöön, sitten , tai .

Vastaus: ,.

Ongelmanratkaisumenetelmien syvempään tutkimiseen, liittyvät yhtälöiden ratkaisemiseen, jotka sisältävät muuttujia moduulimerkin alla, Voit suositella opetusohjelmia suositellun kirjallisuuden luettelosta.

1. Matematiikan tehtäväkokoelma korkeakouluihin hakijoille / Toim. MI. Scanavi. – M.: Rauha ja koulutus, 2013. – 608 s.

2. Suprun V.P. Matematiikka lukiolaisille: monimutkaisempia tehtäviä. – M.: CD “Librocom” / URSS, 2017. – 200 s.

3. Suprun V.P. Matematiikka lukiolaisille: epätyypilliset menetelmät ongelmien ratkaisemiseen. – M.: CD “Librocom” / URSS, 2017. – 296 s.

Onko sinulla vielä kysyttävää?

Jos haluat apua ohjaajalta, rekisteröidy.

verkkosivuilla, kopioitaessa materiaalia kokonaan tai osittain, linkki lähteeseen vaaditaan.

MBOU Secondary School No. 17, Ivanovo

« Yhtälöt moduulilla"
Metodologinen kehitys

Käännetty

matematiikan opettaja

Lebedeva N.V.

20010

Selittävä huomautus

Luku 1. Johdanto

Osa 2. Perusominaisuudet Luku 3. Lukumoduulin käsitteen geometrinen tulkinta Osa 4. Funktio y = |x| Osa 5. Yleissopimukset

Luku 2. Moduulin sisältävien yhtälöiden ratkaiseminen

Osa 1. Yhtälöt muotoa |F(x)| = m (yksinkertaisin) Kappale 2. Yhtälöt muotoa F(|x|) = m Osa 3. Yhtälöt muotoa |F(x)| = G(x) Osa 4. Yhtälöt muotoa |F(x)| = ± F(x) (kaunein) Osa 5. Yhtälöt muotoa |F(x)| = |G(x)| Osa 6. Esimerkkejä epästandardien yhtälöiden ratkaisemisesta Osa 7. Yhtälöt muotoa |F(x)| + |G(x)| = 0 Kappale 8. Yhtälöt muotoa |a 1 x ± in 1 | ± |a 2 x ± in 2 | ± …|a n x ± in n | = m Osa 9. Yhtälöt, jotka sisältävät useita moduuleja

Luku 3. Esimerkkejä erilaisten yhtälöiden ratkaisemisesta moduulilla.

Osa 1. Trigonometriset yhtälöt Osa 2. Eksponentiaaliyhtälöt Osa 3. Logaritmiset yhtälöt Osa 4. Irrationaaliset yhtälöt Osa 5. Edistyneet tehtävät Vastaukset harjoituksiin Viitteet

Selittävä huomautus.

Reaaliluvun itseisarvon (moduulin) käsite on yksi sen olennaisista ominaisuuksista. Tällä konseptilla on laajalle levinnyt fysiikan, matemaattisten ja teknisten tieteiden eri osa-alueilla. Käytännössä matematiikan kurssien opettamisessa toisen asteen oppilaitoksissa Venäjän federaation puolustusministeriön ohjelman mukaisesti käsite "luvun absoluuttinen arvo" kohdataan toistuvasti: 6. luokalla moduulin määritelmä ja sen geometrinen merkitys esitellään; 8. luokalla muodostetaan absoluuttisen virheen käsite, tarkastellaan yksinkertaisimpien moduulin sisältävien yhtälöiden ja epäyhtälöiden ratkaisua ja tutkitaan aritmeettisen neliöjuuren ominaisuuksia; 11. luokalla käsite löytyy osiosta “Juuri n- aste." Opetuskokemus osoittaa, että opiskelijat kohtaavat usein vaikeuksia ratkaista tehtäviä, jotka edellyttävät tämän materiaalin tuntemusta, ja usein ohittavat ne aloittamatta niiden suorittamista. Myös 9. ja 11. luokan kurssien tenttitehtävien tekstit sisältävät vastaavia tehtäviä. Lisäksi vaatimukset, joita yliopistot asettavat valmistuneille, ovat erilaiset, nimittäin korkeammalla tasolla kuin koulun opetussuunnitelman vaatimukset.

Nyky-yhteiskunnan elämälle matemaattisen ajattelutavan muodostuminen, joka ilmenee tietyissä henkisissä taidoissa, on erittäin tärkeä. Moduulien ongelmien ratkaisuprosessissa vaaditaan kykyä käyttää tekniikoita, kuten yleistämistä ja määrittelyä, analysointia, luokittelua ja systematisointia sekä analogiaa. Tällaisten tehtävien ratkaisemisen avulla voit testata tietosi koulukurssin pääosista, loogisen ajattelun tasoa ja alustavia tutkimustaitojasi.

Tämä työ on omistettu yhdelle osista - moduulin sisältävien yhtälöiden ratkaisemisesta. Se koostuu kolmesta luvusta. Ensimmäisessä luvussa esitellään peruskäsitteet ja tärkeimmät teoreettiset näkökohdat. Toisessa luvussa ehdotetaan yhdeksän päätyyppiä moduulin sisältäviä yhtälöitä, käsitellään niiden ratkaisumenetelmiä ja tarkastellaan esimerkkejä eri monimutkaisuusasteista. Kolmas luku tarjoaa monimutkaisempia ja epästandardeja yhtälöitä (trigonometrinen, eksponentiaalinen, logaritminen ja irrationaalinen). Jokaiselle yhtälötyypille on harjoituksia itsenäiseen ratkaisemiseen (vastaukset ja ohjeet ovat liitteenä). .

Tämän työn päätarkoituksena on antaa opettajille metodologista apua oppituntien valmistelussa ja valinnaisten kurssien järjestämisessä. Materiaalia voidaan käyttää myös lukiolaisten opetusapuna. Työssä ehdotetut tehtävät ovat mielenkiintoisia ja ei aina helposti ratkaistavissa, mikä mahdollistaa opiskelijoiden koulutusmotivaation tietoisuuden lisäämisen, kykyjen testaamisen sekä valmistuneiden korkeakouluihin pääsyn valmistuksen lisäämisen. Eriytetty valinta ehdotetuista harjoituksista sisältää siirtymisen materiaalin hallitsemisen lisääntymiseltä luovaan tasoon sekä mahdollisuuden opettaa soveltamaan tietojasi epätyypillisten ongelmien ratkaisemisessa. : Luku 1. Johdanto. Osa 1. Itseisarvon määrittäminen Määritelmä Osa 1. Itseisarvon määrittäminen Reaaliluvun itseisarvo (moduuli). A ei-negatiivista lukua kutsutaan: │ Osa 1. Itseisarvon määrittäminen │ tai

│ -A.

│a│ = │ 0, jos a = 0 (1)

│ - ja jos a
Esimerkkejä: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Laajenna lausekemoduuli:

a) │x - 8│, jos x > 12 b) │2x + 3│, jos x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Osa 2. Perusominaisuudet.

Tarkastellaanpa itseisarvon perusominaisuuksia. Kiinteistö nro 1: Vastakkaisilla luvuilla on samat moduulit, ts. │а│=│- а│ Osoittakaamme, että tasa-arvo on totta. Kirjoita numeron määritelmä muistiin - A : │- a│= (2) Verrataan joukkoja (1) ja (2). Ilmeisesti numeroiden absoluuttisten arvojen määritelmät Osa 1. Itseisarvon määrittäminen Ja - A ottelu. Siten, │а│=│- а│
Kun tarkastellaan seuraavia ominaisuuksia, rajoitamme niiden muotoiluun, koska niiden todisteet on annettu Kiinteistö nro 2: Reaalilukujen äärellisen määrän summan itseisarvo ei ylitä termien itseisarvojen summaa: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Kiinteistö nro 3: Kahden reaaliluvun välisen eron itseisarvo ei ylitä niiden absoluuttisten arvojen summaa: │а - в│ ≤│а│+│в│ Kiinteistö nro 4: Äärillisen määrän reaalilukujen tulon itseisarvo on yhtä suuri kuin tekijöiden itseisarvojen tulo: │а·в│=│а│·│в│ Kiinteistö nro 5: Reaalilukujen osamäärän itseisarvo on yhtä suuri kuin niiden absoluuttisten arvojen osamäärä:

Luku 3. Lukumoduulin käsitteen geometrinen tulkinta.

Jokainen reaaliluku voidaan liittää numeroviivan pisteeseen, joka on tämän reaaliluvun geometrinen kuva. Jokainen numeroviivan piste vastaa sen etäisyyttä origosta, ts. janan pituus origosta tiettyyn pisteeseen. Tätä etäisyyttä pidetään aina ei-negatiivisena arvona. Siksi vastaavan segmentin pituus on geometrinen tulkinta tietyn reaaliluvun itseisarvosta

Esitetty geometrinen kuva vahvistaa selvästi ominaisuuden nro 1, ts. vastakkaisten lukujen moduulit ovat yhtä suuret. Tästä tasa-arvon pätevyys on helposti ymmärrettävissä: │х – а│= │а – x│. Myös yhtälön │х│= m ratkaisu, jossa m ≥ 0, eli x 1,2 = ± m, tulee myös selvemmäksi. Esimerkkejä: 1) │х│ = 4 x 1,2 = ± 4 2) │х - 3│ = 1
x 1,2 = 2; 4

Osa 4. Funktio y = │х│ kuvaaja

Tämän funktion toimialue on kaikki reaaliluvut.

Osa 5. Yleissopimukset.

Jatkossa, kun tarkastellaan esimerkkejä yhtälöiden ratkaisemisesta, käytetään seuraavia sopimuksia: ( - järjestelmän merkki [ - kokonaisuuden merkki Yhtälöjärjestelmää (epäyhtälöjä) ratkaistaessa löydetään järjestelmään sisältyvien yhtälöiden (epäyhtälöiden) ratkaisujen leikkauspiste. Yhtälöjoukkoa (epäyhtälöitä) ratkaistaessa löydetään yhtälöjoukon (epäyhtälöiden) ratkaisujen liitto.

Luku 2. Moduulin sisältävien yhtälöiden ratkaiseminen.

Tässä luvussa tarkastellaan algebrallisia menetelmiä yhden tai useamman moduulin sisältävien yhtälöiden ratkaisemiseksi.

Kappale 1. Yhtälöt muotoa │F (x)│= m

Tämän tyyppistä yhtälöä kutsutaan yksinkertaisimmiksi. Sillä on ratkaisu silloin ja vain jos m ≥ 0. Moduulin määritelmän mukaan alkuperäinen yhtälö vastaa kahden yhtälön joukkoa: │ F(x)│=m
Esimerkkejä:
№1. Ratkaise yhtälö: │7х - 2│= 9


Vastaus: x 1 = -1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│ = 1

x 2 + 3x + 2 = 0 x 2 +3 x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Vastaus: juurien summa on -2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 merkitään x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5 m + 4 = 0 m = 1; 4 – molemmat arvot täyttävät ehdon m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Vastaus: yhtälön 7 juurien lukumäärä. Harjoitukset:
№1. Ratkaise yhtälö ja osoita juurien summa: │х - 5│= 3 №2 . Ratkaise yhtälö ja osoita pienempi juuri: │x 2 + x│= 0 №3 . Ratkaise yhtälö ja osoita suurempi juuri: │x 2 – 5x + 4│= 4 №4 .Ratkaise yhtälö ja osoita koko juuri: │2x 2 – 7x + 6│= 1 №5 .Ratkaise yhtälö ja ilmoita juurien lukumäärä: │x 4 – 13x 2 + 50│= 14

Kappale 2. Yhtälöt muotoa F(│х│) = m

Vasemmalla puolella oleva funktion argumentti on moduulimerkin alla ja oikea puoli on riippumaton muuttujasta. Tarkastellaan kahta tapaa ratkaista tämän tyyppisiä yhtälöitä. 1 tapa: Absoluuttisen arvon määritelmän mukaan alkuperäinen yhtälö vastaa kahden järjestelmän yhdistelmää. Joissa kussakin alimodulaariselle lausekkeelle asetetaan ehto. F(│х│) =m
Koska funktio F(│x│) on parillinen koko määritelmän alueella, yhtälöiden F(x) = m ja F(- x) = m juuret ovat vastakkaisten lukujen pareja. Siksi riittää, että ratkaistaan ​​yksi järjestelmistä (kun tarkastellaan esimerkkejä tällä tavalla, ratkaisu annetaan yhteen järjestelmään). Tapa 2: Uuden muuttujan käyttöönottomenetelmän soveltaminen. Tässä tapauksessa otetaan käyttöön merkintä │x│= a, jossa a ≥ 0. Tämä menetelmä on suunnittelultaan pienempi.
Esimerkkejä: №1 . Ratkaise yhtälö: 3x 2 – 4│x│= - 1 Käytetään uuden muuttujan käyttöönottoa. Merkitään │x│= a, missä a ≥ 0. Saadaan yhtälö 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Paluu alkuperäiseen muuttujaan: │ x│=1 ja │х│= 1/3. Jokaisella yhtälöllä on kaksi juuria. Vastaus: x 1 = 1; X 2 = -1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Ratkaise yhtälö: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
Etsitään ratkaisu perusjoukon ensimmäiseen järjestelmään: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Huomaa, että x 2 ei tyydytä ehto x ≥ 0. Ratkaise toinen järjestelmä on arvon x 1 vastainen luku. Vastaus: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Ratkaise yhtälö: x 4 – │х│= 0 Merkitään │х│= a, missä a ≥ 0. Saadaan yhtälö a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Paluu alkuperäiseen muuttujaan: │х│=0 ja │х│= 1 x = 0; ± 1 Vastaus: x 1 = 0; X 2 = 1; X 3 = - 1.
Harjoitukset: №6. Ratkaise yhtälö: 2│х│ - 4,5 = 5 - 3 / 8 │х│ №7 . Ratkaise yhtälö, ilmoita juurten lukumäärä vastauksessasi: 3x 2 - 7│x│ + 2 = 0 №8 . Ratkaise yhtälö, merkitse vastauksessasi kokonaislukuratkaisut: x 4 + │x│ - 2 = 0

Kappale 3. Yhtälöt muotoa │F(x)│ = G(x)

Tämän tyyppisen yhtälön oikea puoli riippuu muuttujasta ja siksi sillä on ratkaisu silloin ja vain, jos oikea puoli on funktio G(x) ≥ 0. Alkuperäinen yhtälö voidaan ratkaista kahdella tavalla : 1 tapa: Standardi, joka perustuu moduulin julkistamiseen sen määritelmän perusteella ja koostuu vastaavasta siirtymisestä kahden järjestelmän yhdistelmään. │ F(x)│ =G(X)

Tätä menetelmää voidaan rationaalisesti käyttää kompleksisen lausekkeen tapauksessa funktiolle G(x) ja vähemmän kompleksiselle lausekkeelle funktiolle F(x), koska oletetaan, että epäyhtälöt funktion F(x) kanssa ratkaistaan. Tapa 2: Sisältää siirtymisen vastaavaan järjestelmään, jossa ehto asetetaan oikealle puolelle. │ F(x)│= G(x)

Tätä menetelmää on helpompi käyttää, jos funktion G(x) lauseke on vähemmän monimutkainen kuin funktion F(x), koska oletetaan, että epäyhtälö G(x) ≥ 0 on ratkaistu Jos kyseessä on useita moduuleja, tätä menetelmää suositellaan käyttämään toista vaihtoehtoa. Esimerkkejä: №1. Ratkaise yhtälö: │x + 2│= 6 -2x
(1 tapa) Vastaus: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(kaksisuuntainen) Vastaus: Juurien tulo on 3.
№3. Ratkaise yhtälö ja osoita vastauksessasi juurten summa:
│x - 6│ = x 2 - 5x + 9

Vastaus: juurien summa on 4.
Harjoitukset: №9. │x + 4│= - 3x №10. Ratkaise yhtälö, ilmoita ratkaisujen lukumäärä vastauksessasi:│x 2 + x - 1│= 2x – 1 №11 . Ratkaise yhtälö, osoita vastauksessasi juurien tulo:│x + 3│= x 2 + x – 6

Kappale 4. Yhtälöt muotoa │F(x)│= F(x) ja │F(x)│= - F(x)

Tämän tyyppisiä yhtälöitä kutsutaan joskus "kauneimmiksi". Koska yhtälöiden oikea puoli riippuu muuttujasta, ratkaisuja on olemassa jos ja vain, jos oikea puoli on ei-negatiivinen. Siksi alkuperäiset yhtälöt ovat ekvivalentteja epäyhtälöille:
│F(x)│= F(x) F(x) ≥ 0 ja │F(x)│= - F(x) F(x) Esimerkkejä: №1 . Ratkaise yhtälö, merkitse vastauksessasi pienempi kokojuuri: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Vastaus: x = 1№2. Ratkaise yhtälö, ilmoita vastauksessasi välin pituus: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Vastaus: raon pituus on 6.№3 . Ratkaise yhtälö ja ilmoita vastauksessasi kokonaislukuratkaisujen lukumäärä: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Vastaus: 4 kokonaista ratkaisua.№4 . Ratkaise yhtälö ja merkitse vastauksesi suurin juuri:
│4 – x –
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Vastaus: x = 3.

Harjoitukset: №12. Ratkaise yhtälö, ilmoita vastauksessasi koko juuri: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Ratkaise yhtälö ja ilmoita kokonaislukuratkaisujen lukumäärä vastauksessasi: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Ratkaise vastauksessasi kokonaisluku, joka ei ole yhtälön juuri:

Osa 5. Yhtälöt muotoa │F(x)│= │G(x)│

Koska yhtälön molemmat puolet ovat ei-negatiivisia, ratkaisuun sisältyy kaksi tapausta: osamodulaariset lausekkeet ovat etumerkillisesti yhtä suuria tai vastakkaisia. Siksi alkuperäinen yhtälö vastaa kahden yhtälön yhdistelmää: │ F(x)│= │ G(x)│
Esimerkkejä: №1. Ratkaise yhtälö, merkitse vastauksessasi koko juuri: │x + 3│=│2x - 1│
Vastaus: koko juuri x = 4.№2. Ratkaise yhtälö: │ x – x 2 – 1│=│2x – 3 – x 2 │
Vastaus: x = 2.№3 . Ratkaise yhtälö ja osoita vastauksessasi juurien tulo:




Juuriyhtälöt 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Vastaus: juurien tulo on – 0,25. Harjoitukset: №15 . Ratkaise yhtälö ja ilmoita vastauksessasi koko ratkaisu: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Ratkaise yhtälö, merkitse vastauksessasi pienempi juuri:│5x - 3│=│7 - x│ №17 . Ratkaise yhtälö ja osoita vastauksessasi juurten summa:

Osa 6. Esimerkkejä epästandardien yhtälöiden ratkaisemisesta

Tässä osiossa tarkastellaan esimerkkejä epästandardeista yhtälöistä, joita ratkaistaessa lausekkeen itseisarvo paljastuu määritelmän mukaan. Esimerkkejä:

№1. Ratkaise yhtälö, osoita vastauksessasi juurien summa: x · │x│- 5x – 6 = 0
Vastaus: juurien summa on 1 №2. . Ratkaise yhtälö, merkitse vastauksessasi pienempi juuri: x 2 - 4x ·
- 5 = 0
Vastaus: pienempi juuri x = - 5. №3. Ratkaise yhtälö:

Vastaus: x = -1. Harjoitukset: №18. Ratkaise yhtälö ja osoita juurien summa: x · │3x + 5│= 3x 2 + 4x + 3
№19. Ratkaise yhtälö: x 2 – 3x =

№20. Ratkaise yhtälö:

Osa 7. Yhtälöt muotoa │F(x)│+│G(x)│=0

On helppo huomata, että tämän tyyppisen yhtälön vasemmalla puolella on ei-negatiivisten suureiden summa. Siksi alkuperäisellä yhtälöllä on ratkaisu silloin ja vain, jos molemmat termit ovat yhtä aikaa nolla. Yhtälö vastaa yhtälöjärjestelmää: │ F(x)│+│ G(x)│=0
Esimerkkejä: №1 . Ratkaise yhtälö:
Vastaus: x = 2. №2. Ratkaise yhtälö: Vastaus: x = 1. Harjoitukset: №21. Ratkaise yhtälö: №22 . Ratkaise yhtälö ja osoita vastauksessasi juurten summa: №23 . Ratkaise yhtälö ja ilmoita ratkaisujen lukumäärä vastauksessasi:

Kappale 8. Yhtälöt, joiden muoto on │a 1 x + b 1 │±│a 2 x + b 2 │± ... │a n x +b n │= m

Tämän tyyppisten yhtälöiden ratkaisemiseen käytetään intervallimenetelmää. Jos ratkaisemme sen moduulien peräkkäisellä laajentamisella, saamme n järjestelmäsarjoja, mikä on erittäin hankalaa ja hankalaa. Tarkastellaan intervallimenetelmän algoritmia: 1). Etsi muuttuvia arvoja X, jossa jokainen moduuli on yhtä suuri kuin nolla (alimodulaaristen lausekkeiden nollia):
2). Merkitse löydetyt arvot numeroviivalle, joka on jaettu intervalleihin (välien lukumäärä on vastaavasti yhtä suuri kuin n+1 ) 3). Määritä millä merkillä kukin moduuli paljastuu kullakin saadulla aikavälillä (ratkaisua tehdessäsi voit käyttää numeroviivaa merkitsemällä siihen merkit) 4). Alkuperäinen yhtälö vastaa aggregaattia n+1 järjestelmät, joissa kussakin muuttujan jäsenyys on ilmoitettu X yksi intervalleista. Esimerkkejä: №1 . Ratkaise yhtälö ja merkitse vastauksesi suurin juuri:
1). Etsitään alimodulaaristen lausekkeiden nollat: x = 2; x = -3 2). Merkitään löydetyt arvot numeroriville ja määritetään millä merkillä kukin moduuli paljastuu tuloksena olevilla aikaväleillä:
x - 2 x - 2 x - 2 - - + - 3 2 x 2 x + 6 2 x + 6 2 x + 6 - + + 3)
- ei ratkaisuja Yhtälöllä on kaksi juuria. Vastaus: suurin juuri x = 2. №2. Ratkaise yhtälö ja anna vastauksesi koko juuri:
1). Etsitään alimodulaaristen lausekkeiden nollat: x = 1,5; x = -1 2). Merkitään löydetyt arvot numeroriville ja määritetään millä merkillä kukin moduuli paljastuu tuloksena olevilla aikaväleillä: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x - 3 2x - 3 2x - 3 - - +
3).
Viimeisellä järjestelmällä ei ole ratkaisuja, joten yhtälöllä on kaksi juuria. Yhtälöä ratkaiseessasi sinun tulee kiinnittää huomiota toisen moduulin edessä olevaan "-"-merkkiin. Vastaus: koko juuri x = 7. №3. Ratkaise yhtälö, osoita vastauksessasi juurten summa: 1). Etsitään alimodulaaristen lausekkeiden nollat: x = 5; x = 1; x = -2 2). Merkitään löydetyt arvot numeroriville ja määritetään millä merkillä kukin moduuli paljastuu tuloksena olevilla aikaväleillä: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Yhtälöllä on kaksi juuria x = 0 ja 2. Vastaus: juurien summa on 2. №4 . Ratkaise yhtälö: 1). Etsitään alimodulaaristen lausekkeiden nollat: x = 1; x = 2; x = 3. 2). Määritetään millä merkillä kukin moduuli paljastuu tuloksena olevilla aikaväleillä. 3).
Yhdistetään kolmen ensimmäisen järjestelmän ratkaisut. Vastaus: ; x = 5.
Harjoitukset: №24. Ratkaise yhtälö:
№25. Ratkaise yhtälö ja osoita vastauksessasi juurten summa: №26. Ratkaise yhtälö ja merkitse vastauksessasi pienempi juuri: №27. Ratkaise yhtälö ja merkitse vastauksesi suurempi juuri:

Osa 9. Yhtälöt, jotka sisältävät useita moduuleja

Useita moduuleja sisältävät yhtälöt olettavat absoluuttisten arvojen läsnäolon alimodulaarisissa lausekkeissa. Tämän tyyppisten yhtälöiden ratkaisemisen perusperiaate on moduulien peräkkäinen paljastaminen, alkaen "ulkoisesta". Ratkaisun aikana käytetään kohdissa 1, 3 käsiteltyjä tekniikoita.

Esimerkkejä: №1. Ratkaise yhtälö:
Vastaus: x = 1; - 11. №2. Ratkaise yhtälö:
Vastaus: x = 0; 4; - 4. №3. Ratkaise yhtälö ja osoita vastauksessasi juurten tulo:
Vastaus: juurien tulo on – 8. №4. Ratkaise yhtälö:
Merkitään populaation yhtälöt (1) Ja (2) ja harkitse ratkaisua jokaiseen niistä erikseen suunnittelun helpottamiseksi. Koska molemmat yhtälöt sisältävät useamman kuin yhden moduulin, on kätevämpää suorittaa vastaava siirtymä järjestelmäjoukkoon. (1)

(2)


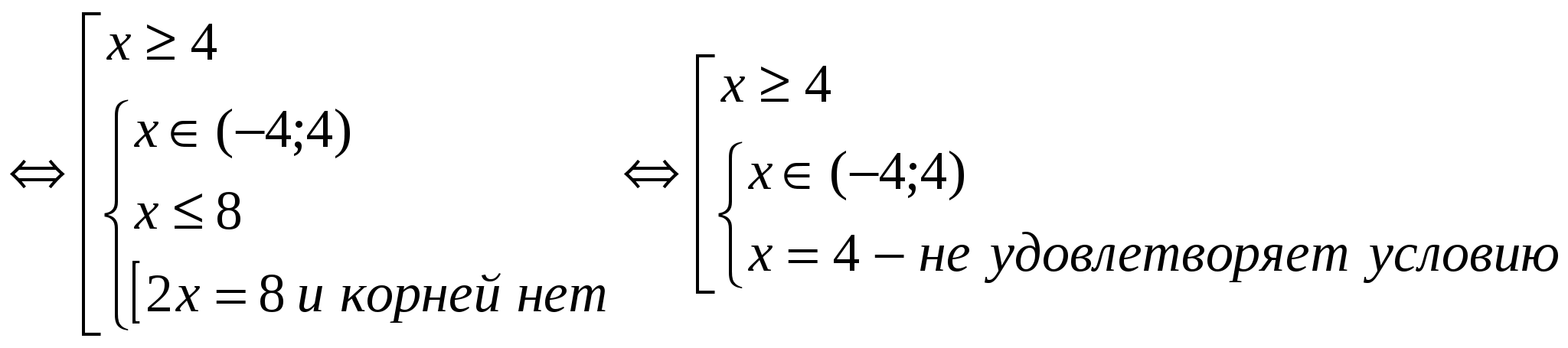Vastaus:
Harjoitukset: №36. Ratkaise yhtälö, osoita vastauksessasi juurien summa: 5 │3x-5│ = 25 x №37. Ratkaise yhtälö, jos juuria on useampi kuin yksi, merkitse vastauksessasi juurien summa: │x + 2│ x – 3x – 10 = 1 №38. Ratkaise yhtälö: 3 │2х -4│ = 9 │х│ №39. Ratkaise yhtälö, ilmoita vastauksessasi juurien lukumäärä per: 2 │ sin x│ = √2 №40 . Ratkaise yhtälö ja ilmoita juurten lukumäärä vastauksessasi:

Osa 3. Logaritmiset yhtälöt.

Ennen kuin ratkaiset seuraavat yhtälöt, sinun on tarkasteltava logaritmien ja logaritmisen funktion ominaisuuksia. Esimerkkejä: №1. Ratkaise yhtälö, osoita vastauksessasi juurien tulo: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ -1

Tapaus 1: jos x ≥ - 1, niin log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – täyttää ehdon x ≥ - 1 2 tapaus: jos x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – täyttää ehdon x - 1
Vastaus: juurien tulo on – 15.
№2. Ratkaise yhtälö, ilmoita vastauksessasi juurten summa: lg
O.D.Z.

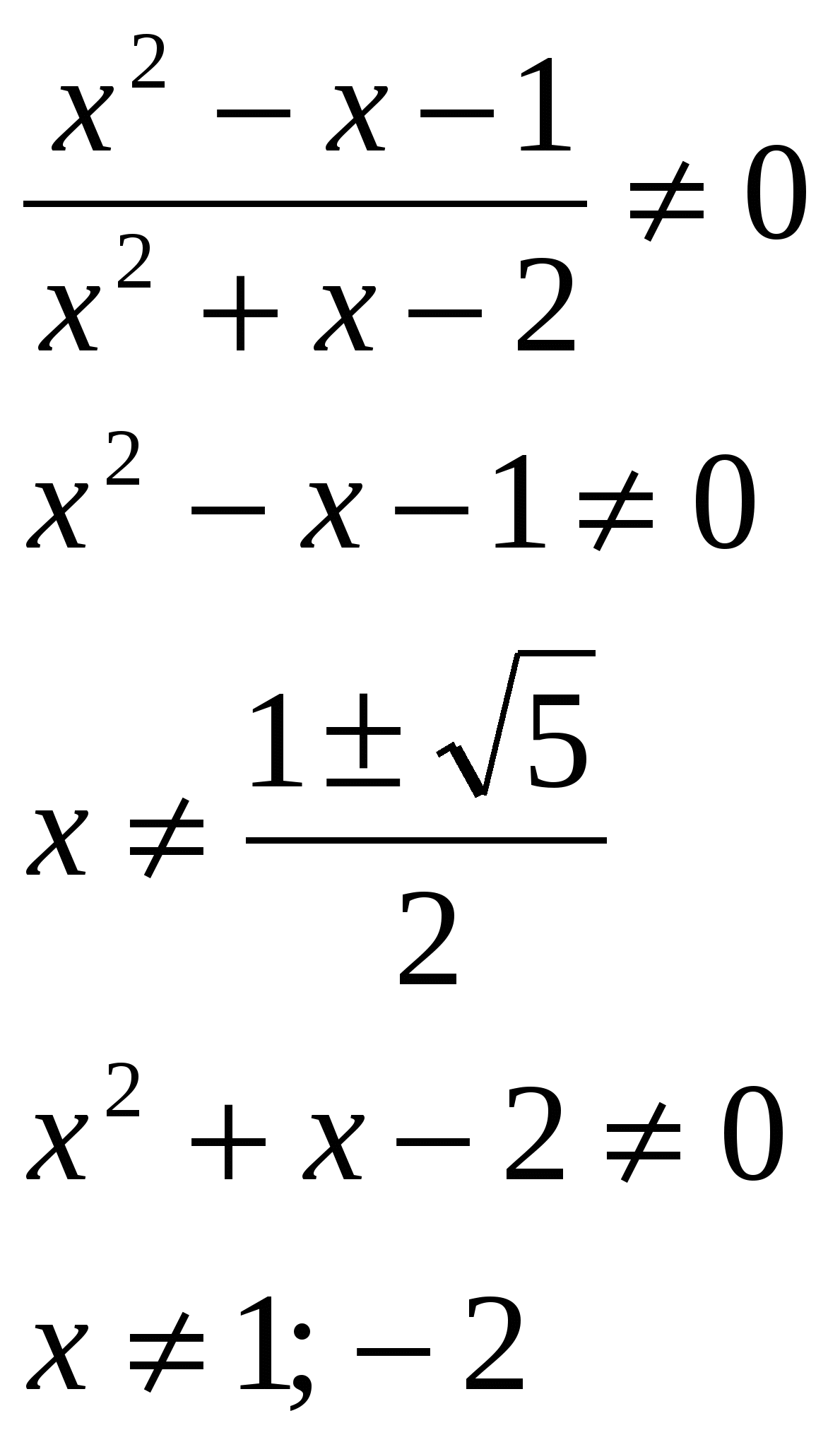
Vastaus: juurien summa on 0,5.
№3. Ratkaise yhtälö: log 5
O.D.Z.

Vastaus: x = 9. №4. Ratkaise yhtälö: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Käytetään kaavaa siirtymiseen toiseen kantaan. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Etsitään alimodulaaristen lausekkeiden nollat: x = 25; x = Nämä luvut jakavat hyväksyttävien arvojen alueen kolmeen väliin, joten yhtälö vastaa kolmen järjestelmän joukkoa.
Vastaus:)